CORRESPONDING ANGLES POSTULATE WORKSHEET

Problem 1 :

In the figure shown below, m∠1 = 105°. Find the measures of the remaining angles.

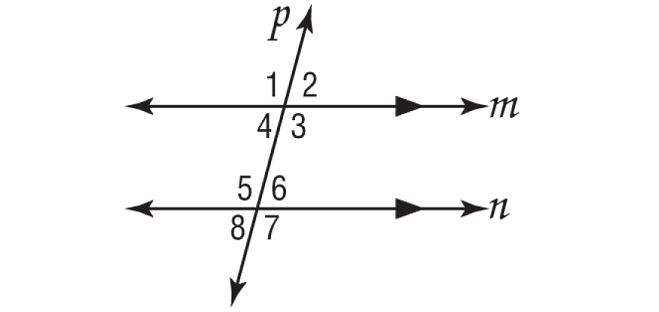
Solution :

∠1 and ∠2 form a linear pair and they are supplementary. 

m∠1 + m∠2  =  180°

105° + m∠2  =  180°

m∠2  =  75°

∠1 and ∠3 are vertical angles and they are equal. 

m∠3  =  m∠1

m∠3  =  105°

∠2 and ∠4 are vertical angles and they are equal. 

m∠4  =  m∠2

m∠4  =  75°

∠1 and ∠5 are corresponding angles and they are equal.

m∠5  =  m∠1

m∠5  =  105°

∠2 and ∠6 are corresponding angles and they are equal.

m∠6  =  m∠2

m∠6  =  75°

∠3 and ∠7 are corresponding angles and they are equal.

m∠7  =  m∠3

m∠7  =  105°

∠4 and ∠8 are corresponding angles and they are equal.

m∠8  =  m∠4

m∠8  =  75°

Problem 2 :

In the figure shown below, m∠2 = 78°. Find the measures of ∠6, ∠10 and ∠14.

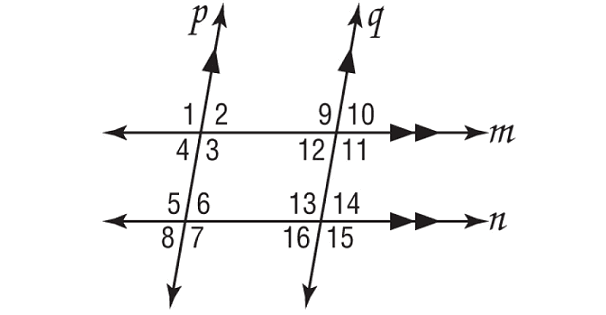
Solution :

In the figure above, lines m and n are parallel, p and q are parallel.

∠2 and ∠6 are corresponding angles and they are equal. 

m∠6  =  m∠2

Substitute m∠2 = 78°.

m∠6  =  78°

∠6 and ∠14 are corresponding angles and they are equal. 

m∠14  =  m∠6

Substitute m∠6 = 78°.

m∠14  =  78°

∠10 and ∠14 are corresponding angles and they are equal. 

m∠10  =  m∠14

Substitute m∠14 = 78°.

m∠10  =  78°

Therefore, 

m∠6  =  78°

m∠10  =  78°

m∠14  =  78°

Problem 3 :

In the figure shown below, lines m and n are parallel and p is transversal. Find the value of x. 

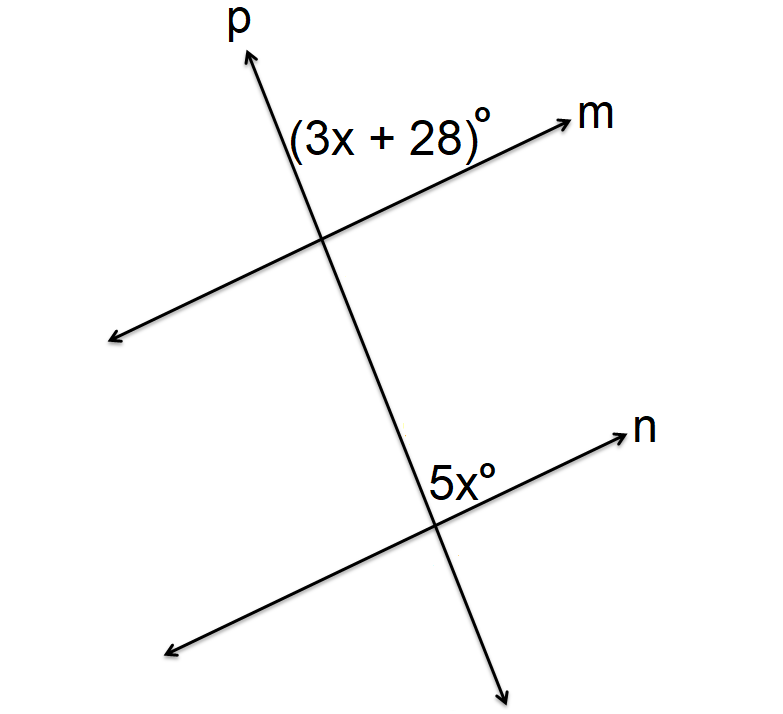
Solution :

In the figure above m and n are parallel and p is transversal. Angles 5x° and (3x + 28)° are corresponding angles and they are equal. 

5x°  =  (3x + 28)°

5x  =  3x + 28

Subtract 3x from each side. 

2x  =  28

Divide each side by 2.

x  =  14

Problem 4 :

In the figure shown below, solve for x. 

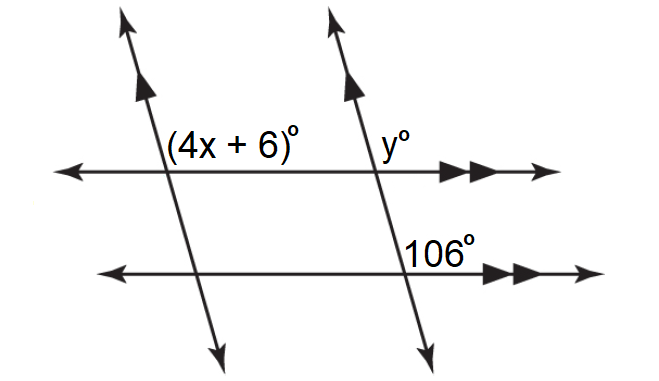
Solution :

In the figure above, two parallel lines are intersected by another two parallel lines.

y° and 106° are corresponding angles and they are equal.

y°  =  106°

(4x + 6)° and y° are corresponding angles and they are equal.

(4x + 6)°  =  y°

Substitute y° = 106°.

(4x + 6)°  =  106°

4x + 6  =  106

Subtract 6 from each side. 

4x  =  100

Divide each side by 4.

x  =  25

Find the angle x in each question below. Give reasons for your answer

Problem 5 :

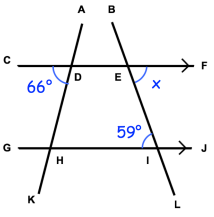
CF and GJ are parallel lines and BL is the transversal.

Alternate interior angles are equal. Then x = 59.

Problem 6 :

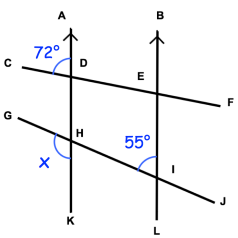
Solution :

AK and BL are parallel lines. Alternate exterior angles are equal. 

<KHI = 72 (alternate exterior angle)

x and 72 linear pairs. Then, x + 72 = 180

x = 180 - 72

x = 108

Problem 7 :

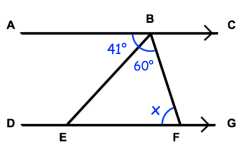
Solution :

AC and DG are parallel lines. Alternate exterior angles are equal. 

<ABE + <EBF + <BFE = 180 (cointerior angles)

41 + 60 + x = 180

101 + x = 180

x = 180 - 101

x = 79

Problem 8 :

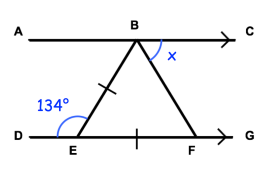
Solution :

<DEB = 134

<DEB and <EBA are co-interior angles.

<EBA = 180 - 134

<EBA = 46

<BEF = 46

Alternate interior angles will  be equal.

<EBF = <EFB

<BEF + <EBF + <EFB = 180

<BEF + <EBF + <EBF = 180

<BEF + 2<EBF = 180

46 + 2<EBF = 180

2<EBF = 180 - 46

2<EBF = 134

<EBF = 134/2

= 67

<ABE + <EBF + <FBC = 180

46 + 67 + x = 180

113 + x = 180

x = 180 - 113

= 67

Problem 9 :

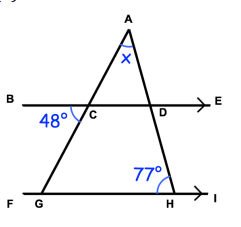
Solution :

BE and FI are parallel lines.

<ACD = 48 (because vertically opposite angles)

<CDA = 77 (Corresponding angles)

In triangle ACD,

<ACD + <CDA + <DAC = 180

48 + 77 + <DAC = 180

125 + <DAC = 180

<DAC = 180 - 125

<DAC = 55 degree

Problem 10 :

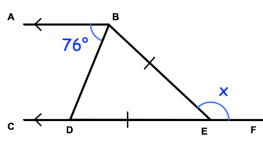
Solution :

CF and AB are parallel lines.

<BDE = <DBA = 76 (alternate interior angles are equal)

<EBD = 76 (Equal sides will make equal angles)

Using exterior angle theorem,

<BEF = <BDE + <EBD

= 76 + 76

= 152

x = 28

So, the value of x is 28 degree.

Problem 11 :

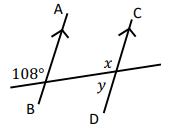
Solution :

AB and CD are parallel lines and 108 and angle x are corresponding angles, they must be equal.

x = 108

x + y = 180

y = 180 - 108

y = 72

Problem 12 :

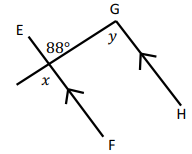
Solution :

EF and GH are parallel lines and x and y are corresponding angles.

x = 88

x = y = 88 (corresponding angles)

Problem 13 :

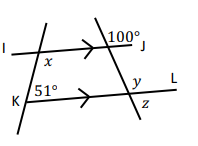
Solution :

IJ and KL are parallel lines and x and 51 are co-interior angles. 

x + 51 = 180

x = 180 - 51

x = 129

100 and y are corresponding angles.

y = 100

y + z = 180

100 + z = 180

z = 180 - 100

z = 80

Problem 14 :

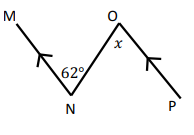
Solution :

x and 62 are alternate interior angles since MN and OP are parallel lines.

x = 62

Problem 15 :

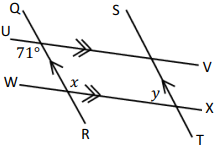
Solution :

Since QR and ST are parallel lines, x and y are corresponding angles.

UV and WX are parallel lines, x and 71 are alternate interior angles. So, they are equal.

x = 71

x + y = 180

71 + y = 180

y = 180 - 71

y = 109

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.