COUNT LINES OF SYMMETRY

When a line divides a given figure into two equal halves such that the left and right halves matches exactly then we say that the figure is symmetrical about the line. This line is called the line of symmetry or axis of symmetry.

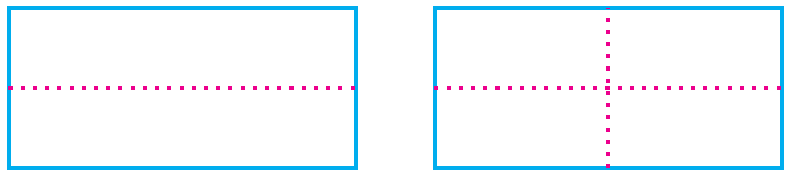
Take a rectangular sheet of paper. Fold it once lengthwise, so that one half fits exactly over the other half and crease the edges. Now open it, and again fold it once along its width.

Example 1 :

For the given regular polygons find the lines of symmetry by using paper folding method and also draw the lines of symmetry by dotted lines.

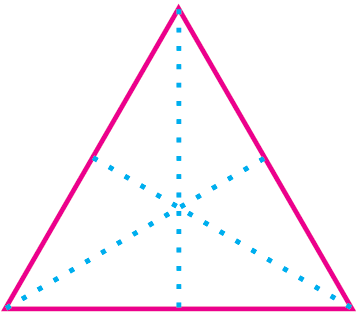
Solution :

By folding the above equilateral triangle along the dotted lines  AF, BD and CE, we will get two symmetric parts.

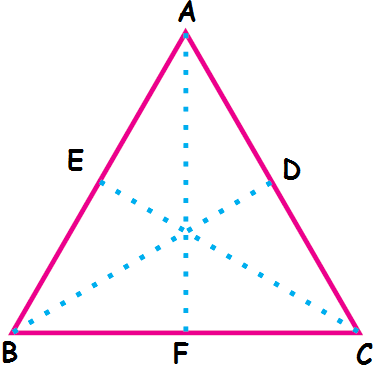
If we fold along the side AF, we will get similar parts ABF and AFC.

If we fold along the side BD, we will get similar parts ABD and BDC.

If we fold along the side CE, we will get similar parts BCE and ACE.

So, an equilateral triangle has three lines of symmetry.

Example 2 :

For the given regular polygons find the lines of symmetry by using paper folding method and also draw the lines of symmetry by dotted lines.

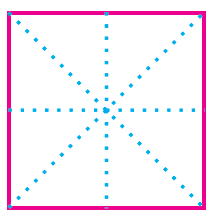
Solution :

By folding the above equilateral triangle along the dotted lines  AE, CG, HD and BF, we will get two symmetric  parts.

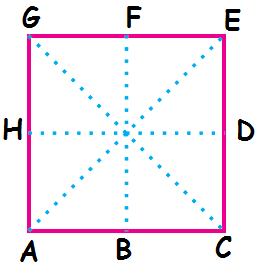
If we fold along the side AE, we will get similar parts ACE and AGE.

If we fold along the side CG, we will get similar parts CAG and CEG.

If we fold along the side HD, we will get similar parts GEDH and ACDH.

If we fold along the side BF, we will get similar parts BCFE and BAGF.

So, a square has four lines of symmetry.

Example 3 :

For the given regular polygons find the lines of symmetry by using paper folding method and also draw the lines of symmetry by dotted lines.

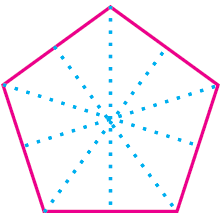
Solution :

By folding the above equilateral triangle along the dotted lines  AF, BG, CH, DI and EJ, we will get two symmetric  parts.

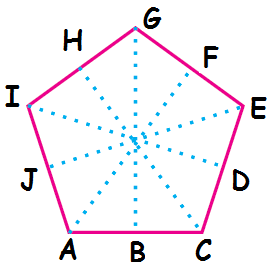
If we fold along the side AF , we will get similar parts ACEF and AIGF.

If we fold along the side BG, we will get similar parts BCEG and BAIG.

If we fold along the side CH, we will get similar parts CEGH and CAIH.

If we fold along the side DI, we will get similar parts DEGI and DCAI.

If we fold along the side EJ, we will get similar parts EGIJ and ECAJ.

So, a regular pentagon has five lines of symmetry.

Example 4 :

For the given regular polygons find the lines of symmetry by using paper folding method and also draw the lines of symmetry by dotted lines.

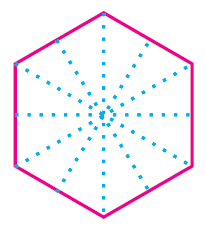
Solution :

By folding the above equilateral triangle along the dotted lines  AF, BH, CI, DJ, EK and GL we will get two symmetric  parts.

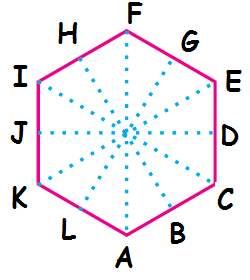
So, a regular hexagon has six lines of symmetry.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.