CRAMER'S RULE OF SOLVING SIMULTANEOUS EQUATIONS

Let us consider the following system of three equations with three unknowns x, y and z. 

a₁₁x + a₁₂y + a₁₃z  =  b₁

a₂₁x + a₂₂y + a₂₃z  =  b₂

a₃₁x + a₃₂y + a₃₃z  =  b₁

Now, we can write the the following determinants using the above equations. 

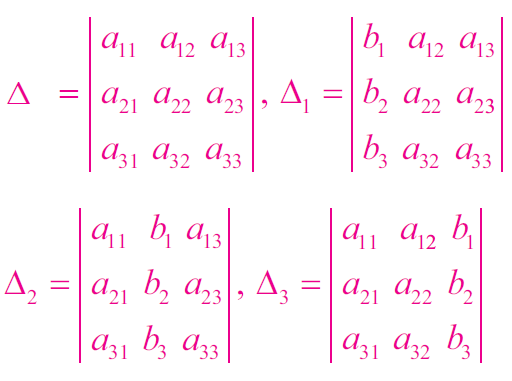
Then, Cramer’s rule to find the values of x, y and z :

x  =  Δ₁/Δ

y  =  Δ₂/Δ

z  =  Δ₃/Δ

If Δ  =  0, the system is inconsistent and it has solution. 

Example 1 :

Solve the following system of linear equations using Cramer’s rule:

5x − 2y + 16  =  0

x + 3y − 7  =  0

Solution :

5x − 2y  =  -16 ------(1) 

x + 3y  =  7 ------(2) 

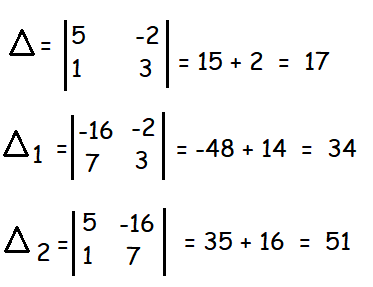
By Cramer's rule, 

x  =  Δ₁/Δ  =  -34/17  =  -2

y  =  Δ₂/Δ  =  51/17  =  3

So, the values of x and y are 2 and 3 respectively.

Example 2 :

Solve the following system of linear equations using Cramer’s rule :

(3/x) + 2y  =  12

(2/x) + 3y  =  13

Solution :

Let 1/x  =  x_1.

Then, 

3x₁ + 2y  =  12

2x₁ + 3y  =  13

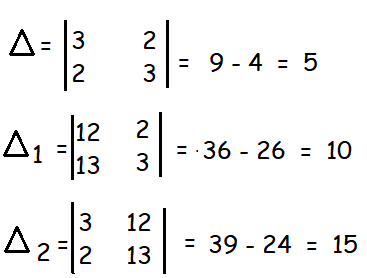
By Cramer's rule, 

x₁  =  Δ₁/Δ  =  10/5  =  2

1/x  =  2 -----> x  =  1/2

y  =  Δ₂/Δ  =  15/5  =  3

So, the values of x and y are 1/2 and 3 respectively.

Example 3 :

Solve the following system of linear equations using Cramer’s rule :

3x + 3y − z  =  11

2x − y + 2z  =  9

4x + 3y + 2z  =  25

Solution :

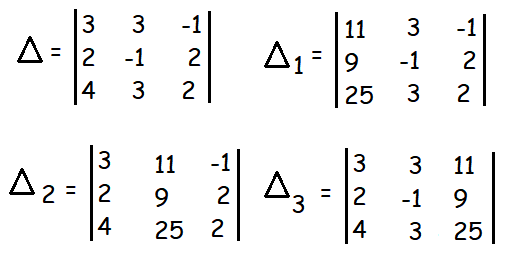
Δ  =  3(-2-6) - 3(4-8) - 1(6+4)

  =  3(-8) - 3(-4) - 1(10)

  =  -24 + 12 - 10

  =  -34 + 12

  =  -22

Δ₁ =  11(-2-6) - 3(18-50) - 1(27+25)

  = 11(-8) - 3(-32) - 1(52)

=  -88 + 96 - 52

=  -140 + 96

Δ₁  =  -44

Δ₂ =  3(18 - 50) - 11(4 - 8) - 1(50 - 36)

  =  3(-32) - 11(-4) - 1(14)

  =  -96 + 44 - 14

  =  -110 + 44

Δ₂  =  -66

Δ₃ =  3(-25 - 27) - 3(50 - 36) + 11(6 + 4)

  =  3(-52) - 3(14) + 11(10)

  =  -156 - 42 + 110

  =  -198 + 110

Δ₃  =  -88

By Cramer's rule, 

x  =  Δ₁/Δ  =  -44/(-22)  =  2

y  =  Δ₂/Δ  =  -66/(-22)  =  3

z  =  Δ₃/Δ  =  -88/(-22)  =  4

So, the values of x, y and z are 2, 3 and 4 respectively.

Example 4 :

Solve the following system of linear equations using Cramer’s rule :

(3/x) - (4/y) - (2/z) - 1  =  0

(1/x) + (2/y) + (1/z) - 2  =  0

(2/x) - (5/y) - (4/z) + 1  =  0

Solution :

Let 1/x  =  a, 1/y  =  b and 1/z  =  c

3a - 4b + 2c  =  1 -----(1)

a + 2b + c  =  2 -----(2)

2a - 5b - 4c  =  -1 -----(3)

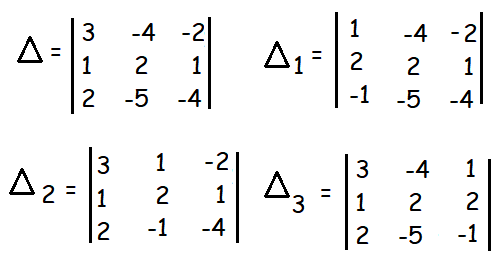
Δ  =  3(-8+5) + 4(-4-2) - 2(-5-4)

  =  3(-3) + 4(-6) - 2(-9)

  =  -9 - 24 + 18

Δ  =  -15

Δ₁ =  1(-8+5) + 4(-8+1) -2(-10+2)

  =  1(-3) + 4(-7) - 2(-8)

  =  -3 - 28 + 16

Δ₁  =  -15

Δ₂  =  3(-8+1) - 1(-4-2) - 2(-1-4)

  =  3(-7) - 1(-6) - 2(-5)

  =  -21 + 6 + 10

  =  -21 + 16

 Δ₂  =  -5

Δ₃ =  3(-2+10) + 4(-1-4) + 1(-5-4)

  =  3(8) + 4(-5) + 1(-9)

  =  24 - 20 - 9

  =  -5

Δ₃  =  -5

By Cramer's rule, 

a  =  Δ₁/Δ  =  -15/(-15)  =  1

b  =  Δ₂/Δ  =  -5/(-15)  =  1/3

c  =  Δ₃/Δ  =  -5/(-15)  =  1/3

Then, 

x  =  1/a  =  1/1  =  1

y  =  1 / (1/3)  =  3

z  =  1 / (1/3)  =  3

So, the values of x, y and z are 1, 3 and 3 respectively. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.