CYCLIC QUADRILATERAL PROBLEMS WITH SOLUTIONS

A cyclic quadrilateral is any four-sided geometric figure whose vertices all lie on a circle.

The opposite angles of a cyclic quadrilateral are supplementary.

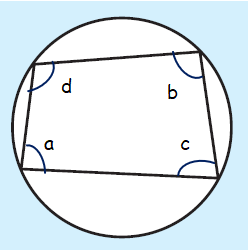
a+b  =  180 and c+d  =  180

One side subtends equal angles at the other two vertices.

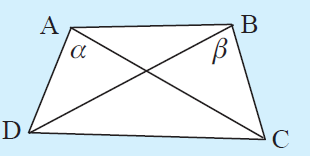
If α = β, then ABCD is a cyclic quadrilateral.

Find the missing angles in the following problems given below.

Example 1 :

Find x given : 

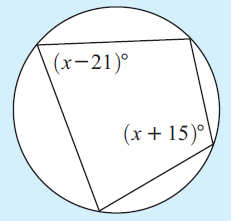
Solution :

In a cyclic quadrilateral, sum of opposite angles are supplementary.

x + 15 + x - 21 = 180

2x - 6 = 180

2x = 186

x = 93

Example 2 :

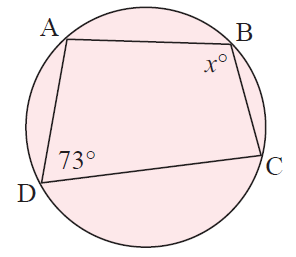
Solution :

73 + x = 180

x = 180-73

x = 107

Example 3 :

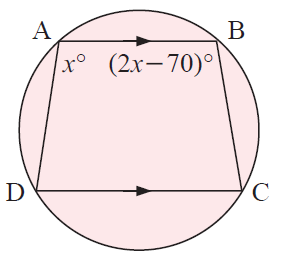
Solution :

x  =  2x - 70

70  =  2x-x

x  =  70

Example 4 :

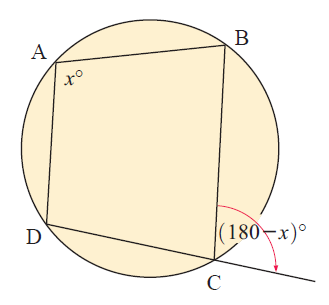
Solution :

Let "y" be <DCB.

<DCB + <BCE  =  180

y + 180 - x  =  180

y-x  =  0  ----(1)

(opposite angles of cyclic quadrilateral)

x+y  =  180   ------(2)

(1)  =  (2)

2y  =  180

y  =  90

So, x is 90.

Example 5 :

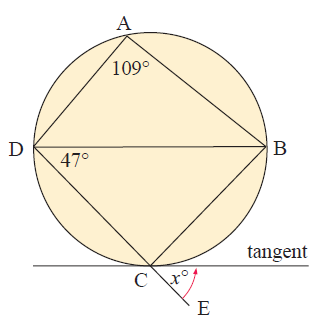
Solution :

<DAB  =  109

<DAB + <DCB  =  180

109 + <DCB  =  180

<DCB  =  180 - 109

<DCB  =  71

In triangle DBC,

<DBC + <DCB + <BDC  =  180

<DBC + 71 + 47  =  180

<DBC  =  180-118

<DBC  =  62

x  =  62

Example 6 :

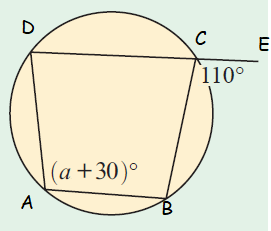
Solution :

Sum of opposite angles are supplementary.

<DAB + <BCD  =  180 

(a+30) + <BCD  =  180  -----(1)

<BCD + <BCE  =  180

<BCD + 110  =  180

<BCD  =  70

By applying the value of <BCD in (1), we get

(a+30) + 70  =  180

a+100  =  180

a  =  80

So, the value of a is 80.

Example 7 :

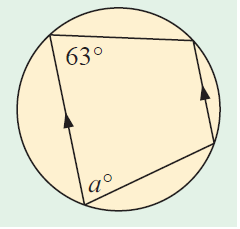
Solution :

Since the two sides are parallel, a and 60 are co-interior angles.

a + 63 = 180

a = 180 - 63

a = 117

So, the missing angle is 117.

Example 8 :

In Figure given below, PQRS is a cyclic quadrilateral whose diagonals intersect at A. If ∠SQR = 80° and ∠QPR = 30°, find ∠SRQ.

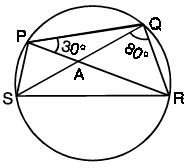
Solution :

∠SQR = 80° and ∠QPR = 30°

∠SPR = 80°

∠SPR + ∠RPQ = 80° + 30°

∠SPQ = 110°

In any cyclic quadrilateral, sum of opposite angles is equal to 180 degree.

∠SRQ = 180° - 110°

∠SRQ = 70°

Example 9 :

PQRS is a cyclic quadrilateral. If ∠Q = ∠R = 65°, find ∠P and ∠S.

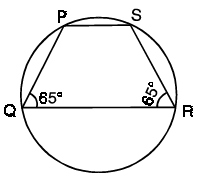
Solution :

Since PS and QR are parallel, the sum of co-interior angles is equal to 180 degree.

∠P + ∠Q = 180

∠P + 65 = 180

∠P = 180 - 65

∠P = 115

Sum of opposite angles is equal to 180 degree.

∠S + ∠Q = 180

∠S + 65 = 180

∠S = 180 - 65

∠S = 115

Example 10 :

In Figure given below, PQRS is a cyclic quadrilateral, and the side PS is extended to the point A. If ∠PQR = 80°, find ∠ASR.

Solution :

∠PQR + ∠PSR = 180

80 + ∠PSR = 180

∠PSR = 180 - 80

∠PSR = 100

∠ASR = 80

Example 11 :

Quadrilateral ABCD is inscribed in circle O, as shown below

If m∠A = 80°, m∠B = 75°, m∠C = (y + 30)°, and m∠D=(x − 10)°, which statement is true?

1) x = 85 and y = 50        2) x = 90 and y = 45

3) x = 110 and y = 75      4) x = 115 and y = 70

Solution :

m∠A + m∠C = 180

∠A + ∠C = 80° + y + 30°

110 + y = 180

y = 180 - 110

y = 70°

m∠B + m∠D = 180

∠B + ∠D = x - 10 + 75

x + 65 = 180

x = 180 - 65

x = 115

So, option (4) is correct.

Example 12 :

In the diagram below, quadrilateral ABCD is inscribed in circle P.

What is m∠ADC?

1) 70°     2) 72°    3) 108°   4) 110°

Solution :

∠ADC + ∠CBA = 180

∠ADC + 72 = 180

∠ADC = 180 - 72

∠ADC = 108

So, option (3) is correct.

Example 13 :

In the diagram below, quadrilateral ABCD is inscribed in circle O, m∠A = (2x)°, m∠B = (x − 10)°, and m∠C = (x + 15)°

What is m∠D?

1) 55°     2) 70°     3) 110°   4) 135°

Solution :

∠C + ∠A = 180

x + 15 + 2x = 180

3x + 15 = 180

3x = 180 - 15

3x = 165

x = 165/3

x = 55

∠D = 180 - (x - 10)

= 180 - (55 - 10)

= 180 - 45

∠D = 135

Example 14 :

In the accompanying diagram, quadrilateral ABCD is inscribed in circle O. If measure of arc AB = 132 and measure of arc BC = 82, find m∠ADC

Solution :

Angle measure created at the center is twice the angle measure at any circumference of the circle.

∠ADC = (132 + 82)/2

= 107

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.