DE MORGANS LAW FOR SET DIFFERENCE

De morgans law for set difference :

Here we are going to see De morgan's law for set difference.

Demorgans law :

De Morgan’s father (a British national) was in the service of East India Company, India. Augustus De Morgan (1806-1871) was born in Madurai, Tamilnadu, India. His family moved to England when he was seven months old. He had his education at Trinity college, Cambridge, England.

De Morgan’s laws relate the three basic set operations union, intersection and complement.

De morgan's laws

De morgan's law for set difference :

For any three sets A, B and C, we have 

(i)  A \ (B u C)  =  (A \ B) n (A \ C)

(ii)  A \ (B n C)  =  (A \ B) u (A \ C)

Proof by Venn diagram

(i)  A \ (B n C)  =  (A \ B) u (A \ C)

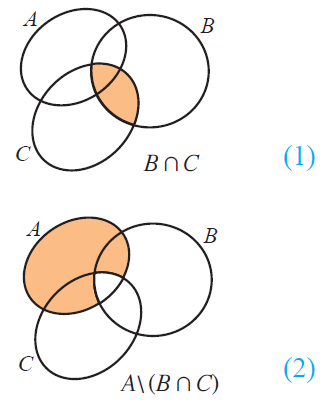
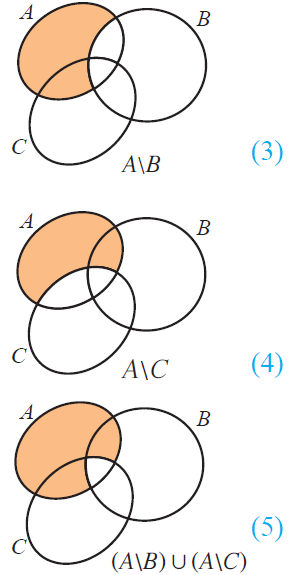
From the above Venn diagrams (2) and (5), it is clear that 

A \ (B n C)  =  (A \ B) u (A \ C)

Hence, De morgan's law for set difference is verified.

(ii)  A \ (B u C)  =  (A \ B) n (A \ C)

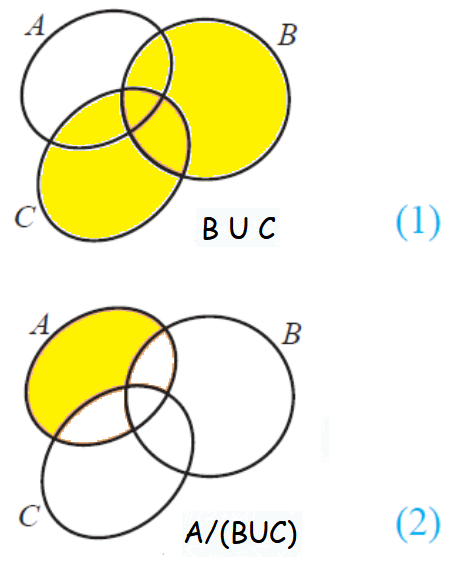
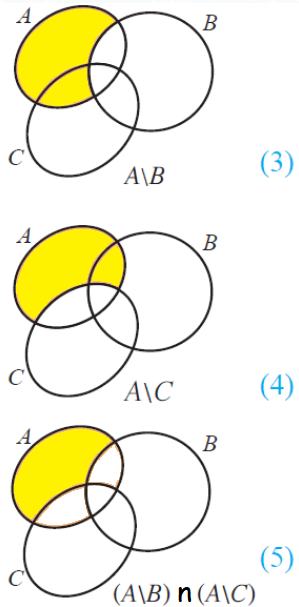
Example 1 : 

Let A  =  { a, b, c, d, e, f, g, x, y, z }, B  =  { 1, 2, c, d, e } and C  =  { d, e, f, g, 2, y }. Verify De Morgan’s laws of set difference.

Solution : 

First, we shall verify A \ (B u C)  =  (A \ B) n (A \ C)

To do this, we consider

B u C  =  { 1, 2, c, d, e } u { d, e, f, g, 2, y }

B u C  =  { 1, 2, c, d, e, f, g, y }

We know that

A/(B u C) =  {a, b, c, d, e, f, g, x, y, z}\{1, 2, c, d, e, f, g, y}

A / (B u C)  =  { a, b, x, z } ---------(1)

A \ B   =  { a, b, f, g, x, y, z }

A \ C   =  { a, b, c, x, z }

(A \ B) n (A \ C)  =  { a, b, x, z } ---------(2)

From (1) and (2), it is clear that A\(B u C)  =  (A\B)n(A\C)

Example 2 :

Let A = {10,15, 20, 25, 30, 35, 40, 45, 50}, B = {1, 5,10,15, 20, 30} and C = {7, 8,15,20,35,45, 48}. Verify A \(B n C) = (A \ B) U (A \ C).

Solution :

First, we shall verify A \ (B u C)  =  (A \ B) n (A \ C)

To do this, we consider

B u C  = {1, 5, 10, 15, 20, 30} U {7, 8, 15, 20, 35, 45, 48}

B u C  =  { 1, 5, 7, 8, 10, 15 , 20,30, 35, 45, 48 }

We know that

A \ (B u C) =  {10,15, 20, 25, 30, 35, 40, 45, 50}\{ 1, 5, 7, 8, 10, 15 , 20,30, 35, 45, 48 }

A / (B u C)  =  { 25, 40, 50 } ---------(1)

A\B = {10, 15, 20, 25, 30, 35, 40, 45, 50}\{1, 5, 10, 15, 20, 30}

  =  {25, 35, 40, 45, 50}

A\C = {10, 15, 20, 25, 30, 35, 40, 45, 50}\ {7, 8, 15, 20, 35, 45, 48}

  =  {25, 30, 40, 50}

(A\B) U (A\C) = { 25, 40, 50} ---------(2)

From (1) and (2), it is clear that A\(B n C)  =  (A\B)u(A\C)

Example 3 :

If A⋂B = {1, 0, −1} and A⋂C = {0, −1, 2, 3}, then find A⋂(B⋃C).

Solution :

A⋂B = {1, 0, −1} and A⋂C = {0, −1, 2, 3}

• Elements in the set A and B are {1, 0, -1}
• Elements in the set A and C are {0, −1, 2, 3}

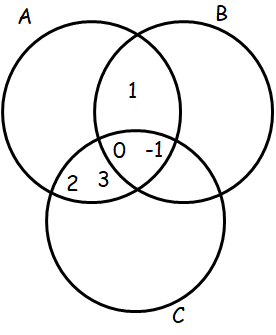
A = {1, 0, 2, 3, -1}

B = {1, 0, -1}

C = {0, -1, 2, 3}

BUC = {-1, 0, -1,  2, 3}

An (BUC) = {-1, 0, -1,  2, 3}

Example 4 :

Let U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4, 5}, B = {0, 2, 1, 6, 8} and C = {3, 6, 9}.

Then find:

a)  A'      b) B\A     c) A ⋂ C'

d) C × (A⋂B)      e) (B\A) × C

Solution :

U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

A = {1, 2, 3, 4, 5}

B = {0, 2, 1, 6, 8} and C = {3, 6, 9}

a) A'

Exclude the elements of A from U.

A' = {0, 6, 7, 8, 9}

b) B\A

=  {0, 2, 1, 6, 8} \ {1, 2, 3, 4, 5}

The common elements in these two sets are 1 and 2. Excluding these elements from B and write the remaining elements in set B.

= {0, 6, 8}

c) A ⋂ C'

To find C', we have to exclude the values of C and write the remaining elements from set U.

C' = {0, 1, 2, 4, 5, 7, 8}

AnC' 

A = {1, 2, 3, 4, 5} and C' = {0, 1, 2, 4, 5, 7, 8}

Common elements of A and C'

= {1, 2, 4, 5}

d) C × (A⋂B)

A⋂B = {1, 2, 3, 4, 5} ⋂ {0, 2, 1, 6, 8}

= {1, 2}

C × (A⋂B) = {3, 6, 9} x {1, 2}

= {(3, 1) (3, 2) (6, 1) (6, 2) (9, 1) (9, 2)}

e) (B\A) × C

(B\A) = {0, 2, 1, 6, 8} \ {3, 6, 9}

= {0, 2, 1, 8}

(B\A) × C = {0, 2, 1, 8} x {3, 6, 9}

= {(0, 3) (0, 6) (0, 9) (2, 3) (2, 6) (2, 9) (1, 3) (1, 6) (1, 9)(8, 3) (8, 6) (8, 9)}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.