DEGREE OF AN ALGEBRAIC EXPRESSION

Let us briefly recap the construction of an algebraic expression. To construct an algebraic expression, we use mathematical operators like addition, subtraction, multiplication and division to combine variables and constants.

Consider the algebraic expression (5y + 7), which can be obtained by multiplying the variable y with the constant 5 and then adding the constant 7 to the product.

To know the degree of an expression, first let us try to understand the degree of a variable by relating it with the exponents of numbers.

Let us consider the square numbers. They have different base and same exponents. The geometrical representation of square numbers are given below.

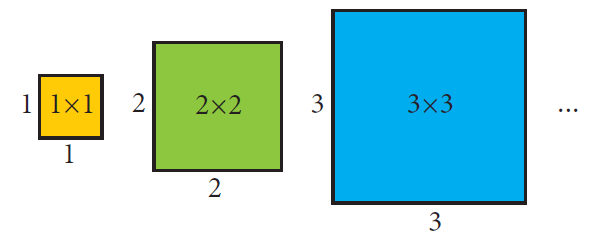
In general, if we consider the side of a square as a variable ‘y’ then its area will be (y x y) sq. units. This can be denoted as ‘y²’. Thus we have an algebraic expression with exponent notation.

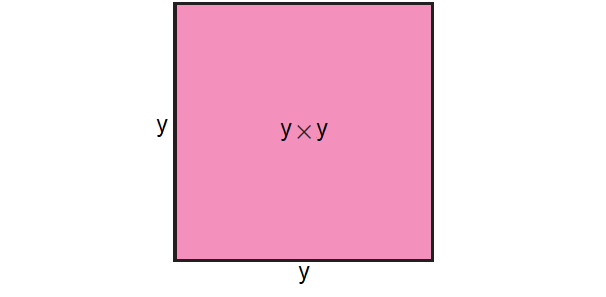
If we consider the term x² as a monomial expression, the highest power of the expression is its exponent, that is 2.
Similarly, when length l units and width w units are variables of a rectangle, then its area is

l x w = lw sq. units.

We can consider lw as a term in an algebraic expression,  where l and w are factors of lw. The highest power of the expression lw is also 2, as we have to add up the powers of the variable factors.

Let us consider an algebraic expression : x³ - 3x² + 4.

The terms of the above expression are x³, -3x² and 4. Exponent of the term x³ is 3 and -3x² is 2. Thus, the term x³ has the highest exponent, that is 3. 

Now, consider the expression, 3x⁴ - 4x³y² + 8xy + 7. 

Take each term and check its power. In 3x⁴, exponent is 4, hence its degree is 4. In -4x³y², the sum of powers of x and y is 5, hence its degree is 5. In 8xy, the sum of powers is 2. Therefore, the term with highest power in the above expression is -4x³y² and its power is 5, which is called as degree of this expression.

The term(s) containing the highest power of the variables in an expression is called the degree of expression.

The degree of any term in an expression can only be a positive integer. Also, degree of expression doesn’t depend on the number of terms, but on the power of variables in the individual terms. The degree of constant term is 0.

Try These

1. Complete the following table:

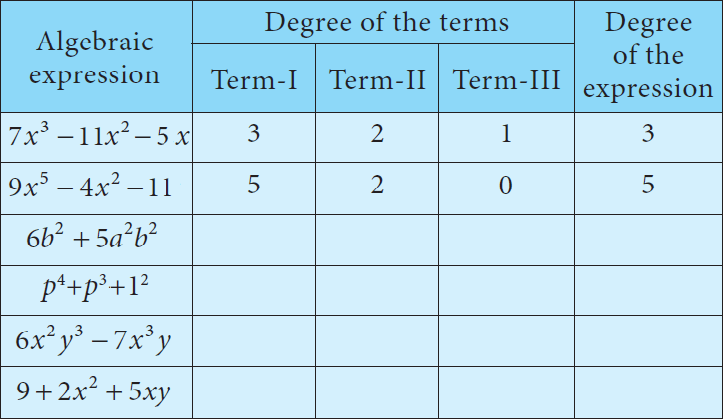
2. Identify the like terms from the following :

(i) 2x²y, 2xy², 3xy², 14x²y, 7yx
(ii) 3x²y², y³x, y³x², -y³x, 3y³x
(iii) 11pq, -pq, 11pqr, -11pq, pq

Solved Problems

Problems 1-5 : In each case, find the degree of the given expression.

Problem 1 :

x⁵

Solution :

In x⁵, the exponent is 5. Thus, the degree of the expression is 5.

Problem 2 :

-3p³q²

Solution :

In -3p³q², the sum of powers of p and q is 5

That is,

3 + 2 = 5

Thus, the degree of the expression is 5.

Problem 3 :

-4xy²z³

Solution :

In -4xy²z³, the sum of powers of x, y and z is 6.

That is,

1 + 2 + 3 = 6

Thus, the degree of the expression is 6.

Problem 4 :

12xyz - 3x³y²z + z⁸

Solution :

The terms of the given expression are 12xyz, -3x³y²z and z⁸.

Degree of each of the terms : 3, 6, 8.

Terms with highest degree : z⁸.

Therefore, degree of the expression is 8.

Problem 5 :

3a³b⁴ - 16c⁶ + 9b²c⁵ + 7 

Solution :

The terms of the given expression are 3a³b⁴, -16c⁶, 9b²c⁵, 7.

Degree of each of the terms : 7, 6, 7, 0.

Terms with highest degree : 3a³b⁴, 9b²c⁵

Therefore, degree of the expression is 7.

Problem 6 :

Add the expressions 4x² + 3xy + 9y² and 2x² - 9xy + 6y²  and find the degree.

Solution :

= (4x² + 3xy + 9y²) + (2x² - 9xy + 6y²)

= 4x² + 3xy + 9y² + 2x² - 9xy + 6y²

Group like terms together.

= (4x² + 2x²) + (3xy - 9xy) + (9y² + 6y²)

= 6x² + (-3xy) + 15y²

= 6x² - 3xy + 15y²

Thus, the degree of the expression is 2.

Problem 7 :

Subtract (x³ - x² + x + 3) from (3x³ - 2x² - 7x + 6) and find the degree.

Solution :

= (3x³ - 2x² - 7x + 6) - (x³ - x² + x + 3)

Distributive the negative sign.

= 3x³ - 2x² - 7x + 6 - x³ + x² - x - 3

Group like terms together.

= (3x³ - x³) + (-2x² + x²) + (-7x - x) + (6 - 3)

Combine like terms.

= 2x³ + (-x²) + (-8x) + 3

= 2x³ - x² - 8x + 3

Hence, the degree of the expression is 3.

Problem 8 :

Simplify and find the degree of the resulting expression.

(4m² + 3n) - (3m + 9n²) - (3m² - 6n²) + (5m - n)

Solution :

= (4m² + 3n) - (3m + 9n²) - (3m² - 6n²) + (5m - n)

= 4m² + 3n - 3m - 9n² - 3m² + 6n² + 5m - n  

Group like terms together.

= (4m² - 3m²) + (-9n² + 6n²) + (-3m + 5m) + (3n - n)

Combine like terms.

= m² + (-3n²) + 2m + 2n

= m² - 3n² + 2m + 2n

Hence, the degree of the expression is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.