DENSENESS PROPERTY OF RATIONAL NUMBERS

Consider a, b where a > b and their arithmetic mean is given by

(a + b) / 2

Is this arithmetic mean a rational number ? Let us see.

If

a  =  p/q (p, q are integers and q ≠ 0) ;

b  =  r/s (s, s are integers and s ≠ 0), 

then

(a + b) / 2  =  (p/q + r/s) / 2  =  (ps + qr) / 2qs

which is a rational number. 

We have to show that this rational number lies between a and b.

a - [(a + b)/2]  =  (2a - a - b)/2  =  (a - b)/2 which is > 0

because a > b.

Therefore, 

a  >  (a + b)/2 -----(1)

[(a + b)/2] - b  =  (a + b - 2b)/2  =  (a - b)/2 which is > 0

Therefore, 

(a + b)/2  >  b -----(2)

From (1) and (2) we see that 

a  >  (a + b)/2  >  b, 

which can be visualized as follows :

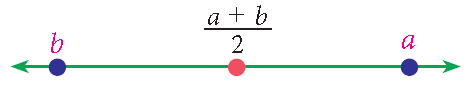
Thus, for any two rational numbers, their average/mid point is rational. Proceeding similarly, we can generate infinitely many rational numbers.

Example : 

Find any two rational numbers between 1/2 and 2/3. 

Solution : 

A rational number between 1/2 and 2/3 is 

=  1/2 ⋅ (1/2 + 2/3)

=  1/2 ⋅ [(3 + 4) / 6]

=  1/2 ⋅ 7/6

=  7/12

A rational number between 1/2 and 7/12 is 

=  1/2 ⋅ (1/2 + 7/12)

=  1/2 ⋅ [(6 + 7) / 12]

=  1/2 ⋅ 13/12

=  13/24

So, two rational numbers between 1/2 and 2/3 are 7/12 and 13/24 (of course, there are more!).

There is an interesting result that could help you to write instantly rational numbers between any two given rational numbers.

Result : 

If p/q and r/s are any two rational numbers such that 

p/q  <  r/s, 

then (p + r)/(q + s) is a rational number, such that

p/q  <  (p + r)/(q + s)  <  r/s

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.