DERIVATIVE OF ABSOLUTE VALUE FUNCTION
Let |f(x)| be an absolute value function.
Then the formula to find the derivative of |f(x)| is given below.
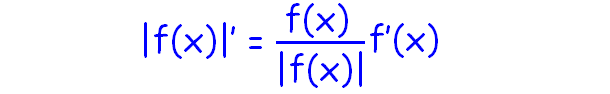
Based on the formula given, let us find the derivative of |x|.
|x|' = (ˣ⁄|ₓ|)(x)'
|x|' = (ˣ⁄|ₓ|)(1)
|x|' = ˣ⁄|ₓ|
Therefore, the derivative of |x| is ˣ⁄|ₓ|.
Let y = |x|'.
Then, we have y = ˣ⁄|ₓ|.
In y = ˣ⁄|ₓ|, if we substitute x = 0, the denominator becomes zero.
Since the denominator becomes zero, y becomes undefined at x = 0
Let us substitute some random values for x in y.
when x = -3,
y = -³⁄|₃| = -³⁄₃ = -1
when x = -2,
y = -²⁄|₂| = -²⁄₂ = -1
when x = -1,
y = -¹⁄|₁| = -¹⁄₁ = -1
when x = 0,
y = 0/|0| = 0/0 = undefined
when x = 1,
y = ¹⁄|₁| = ¹⁄₁ = 1
when x = 2,
y = ²⁄|₂| = ²⁄₂ = 1
when x = 3,
y = ³⁄|₃| = ³⁄₃ = 1
Let us summarize the above calculation in table.
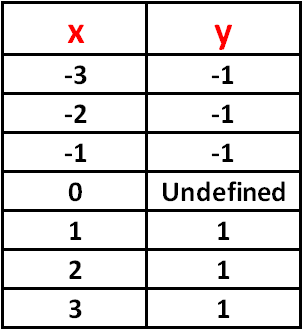
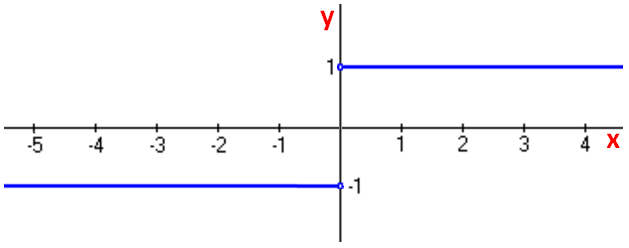
Now, based on the table given above, we can get the graph of derivative of |x|.
Find the derivative of each of the following absolute value functions.
Example 1 :
|2x + 1|
Solution :
Example 2 :
|x3 + 1|
Solution :
Example 3 :
|x|3
Solution :
In the given function |x|3, using chain rule, first we have to find derivative for the exponent 3 and then for |x|.
Example 4 :
|x2 - 5x + 6|
Solution :
Example 5 :
|2x - 5|
Solution :
Example 6 :
(x - 2)2 + |x - 2|
Solution :
Example 7 :
3|5x + 7|
Solution :
Example 8 :
|sinx|
Solution :
Example 9 :
|cosx|
Solution :
Example 10 :
|tanx|
Solution :
Example 11 :
|sinx + cosx|
Solution :
Example 12 :
|cscx|
Solution :
Example 13 :
|secx|
Solution :
Example 14 :
|cotx|
Solution :
Example 15 :
|lnx|
Solution :
Example 16 :
|ex|
Solution :
Example 17 :
|√x|
Solution :
Example 18 :
Solution :
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 72)
Nov 23, 24 09:36 PM
Digital SAT Math Problems and Solutions (Part - 72) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 23, 24 10:01 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 76)
Nov 23, 24 09:45 AM
Digital SAT Math Problems and Solutions (Part - 76)
