DERIVATIVE OF ABSOLUTE VALUE OF SIN X

In this section, we will learn, how to find the derivative of absolute value of (sinx). 

Let |f(x)| be the absolute-value function. 

Then the formula to find the derivative of |f(x)| is given below. 

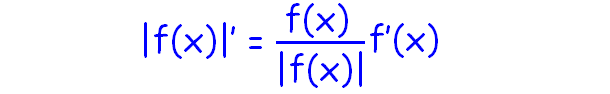
Based on the formula given, let us find the derivative of absolute value of sinx.

Derivative of |sinx| :

|sinx|'  =  [sinx/|sinx|] ⋅ (sinx)'

|sinx|'  = [sinx/|sinx|] ⋅ cosx

|sinx|'  =  (sinx ⋅ cosx) / |sinx|

Derivative of Absolute Value of Other Trigonometric Functions

Derivative of |cosx| :

|cosx|'  =  [cosx/|cosx|] ⋅ (cosx)'

|cosx|'  =  [cosx/|cosx|] ⋅ (-sinx)

|cosx|'  =  - (sinx ⋅ cosx) / |cosx|

Derivative of |tanx| :

|tanx|'  =  [tanx/|tanx|] ⋅ (tanx)'

|tanx|'  = [tanx/|tanx|] ⋅ sec²x

|tanx|'  =  sec²x ⋅ tanx / |tanx|

Derivative of |cscx| :

|cscx|'  =  [cscx/|cscx|] ⋅ (cscx)'

|cscx|'  =  [cscx/|cscx|] ⋅ (-cscx ⋅ cotx)

|cscx|'  =  - (csc²x ⋅ cotx) / |cscx|

Derivative of |secx| :

|secx|'  =  [secx/|secx|] ⋅ (secx)'

|secx|'  =  [secx/|secx|] ⋅ (secx ⋅ tanx)

|secx|'  =  - (sec²x ⋅ tanx) / |secx|

Derivative of |cotx| :

|cotx|'  =  [cotx/|cotx|] ⋅ (cotx)'

|cotx|'  =  [cot/|cotx|] ⋅ (-csc²x)

|cotx|'  =  - (csc²x ⋅ cotx) / |cotx|

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.