DERIVATIVES USING PRODUCT RULE WITH EXAMPLES

Let u and v be two differentiable functions. Then

d(uv)/dx  =  u (dv/dx) + v (du/dx)  (or)

d(uv)/dx  =  u v' + v u'

Question 1 :

Differentiate y = x sin x cos x

Solution :

Let u  =  x ==>  u'  =  1

v  =  sin x  ==> v'  =  cos x

w  =  cos x  ==>  w'  =  -sin x

d (uvw)  =  u'v w + u v'w + u v w' 

dy/dx  =  1 (sin x)(cos x) + x (cos x) (cos x) + x sinx (-sinx)

  =  sin x cos x + x cos²x - x sin²x

  =  sin x cos x + x (cos²x - sin²x)

  =  sin x cos x + x cos 2x

Question 2 :

Differentiate y = e^-x log x

Solution :

Let u  =  e^-x ==>  u'  =  -e^-x

v  =  log  x  ==> v'  =  1/x

d(uv)  =  u v' + v u'

  =  e^-x (1/x) + log x(-e^-x)

  =  e^-x [(1/x) - log x]

Question 3 :

Differentiate y = (x² + 5) log (1 + x) e^-3x

Solution :

Let u  =  x² + 5 ==>  u'  =  2x

v  =  log (1 + x)  ==> v'  =  1/(1 + x)

w  =  e^-3x  ==>  w'  =  -3 e^-3x

d (uvw)  =  u'v w + u v'w + u v w' 

dy/dx 

=  2x(log (1+x))e^-3x+(x²+5)(1/(1+x))e^-3x+(x²+5)log (1+x) (-3e^-3x)

=  e^-3x[2x(log (1+x))+(x²+5)/(1+x)-3(x²+5)log (1+x)] 

Question 4 :

Differentiate y = sin x°

Solution :

We know that 1 degree= π/180 radian

so,x degrees= πx/180 radian

Now, the expression is : y = sin( πx/180).

then, dy/dx= π/180.cos( πx/180).

Question 5 :

Differentiate y = log₁₀ x

Solution :

y = log₁₀ x

dy/dx  =  (1/x)log₁₀e  

dy/dx  =  log₁₀e / x

Question 6 :

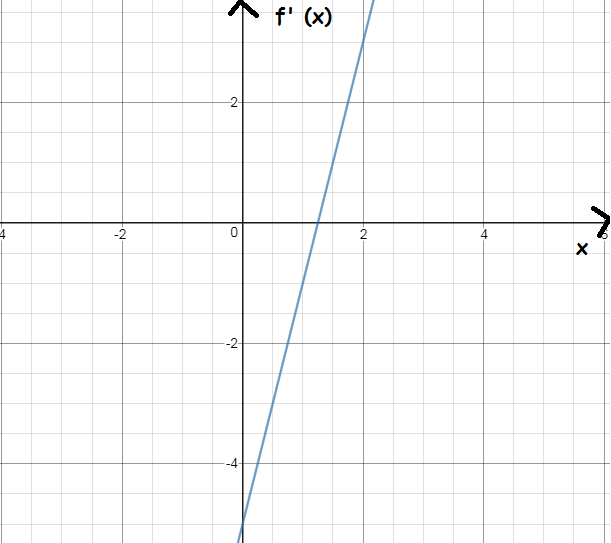
Draw the function f '(x) if f (x) = 2x² − 5x + 3

Solution :

f (x) = 2x² − 5x + 3

f'(x)  =  2(2x) - 5(1) + 0

f'(x)  =  4x - 5

When x = 0, f'(0)  =  -5

When f'(x)  =  0, 4x - 5  =  0  ==>  x  =  5/4  =  1.25  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.