DETERMINANT METHOD OF SOLVING LINEAR EQUATIONS

To solve system of linear equations in two variable, we use the following rules.

Example 1 :

Solve the  following equation using determinant method

x + 2y  =  3, x + y  =  2

Solution :

Write the values of Δ, Δx and Δy and evaluate

Here Δ  ≠  0, Δx ≠ 0 and Δy ≠ 0.

So, the system is consistent and it has unique solution.

x  =  Δx/Δ and y = Δy/Δ

x  =  -1/(-1)  ==>  1

x  =  -1/(-1)  ==>  1

Hence the solution is (1, 1).

Example 2 :

Solve the  following equation using determinant method

3x + 2y  =  5 and  x + 3y  =  4

Solution :

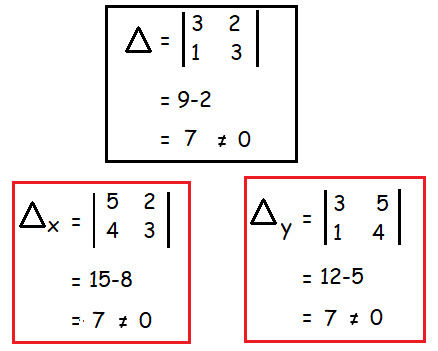
Here Δ  ≠  0, Δx ≠ 0 and Δy ≠ 0.

So, the system is consistent and it has unique solution.

x  =  Δx/Δ and y = Δy/Δ

x  =  7/7  ==>  1

x  =  7/7  ==>  1

Hence the solution is (1, 1).

Example 3 :

Solve the  following equation using determinant method

x + 2y = 3  and 2x + 4y = 8

Solution :

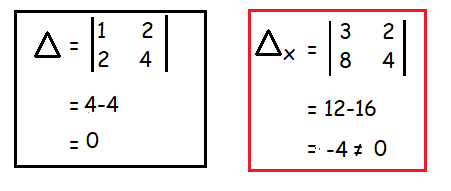
Here, Δ  = 0 but Δx ≠ 0.

So, the system is inconsistent and it has no solution.

Example 4 :

Solve the  following equation using determinant method

x + 2y = 3 and 2x + 4y = 6

Solution :

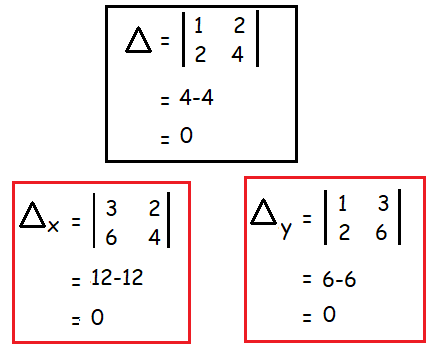
Since ∆ = 0, ∆ₓ = 0 and  ∆ᵧ = 0 and atleast one of the element in ∆ is non zero.

Then the system is consistent and it has infinitely many solution. The above system is reduced into one equation. To solve this equation we have to assign y = k.

x+2y  =  3

x+2(k)  =  3

x+2k  =  3

x  =  3-2k and y  =  k

So, the solution is (3-2k, k). Here k ∈ R where R is real numbers.

Example 5 :

Solve the  following equation using determinant method

2x+4y  =  6,  6x+12y  =  24

Solution :

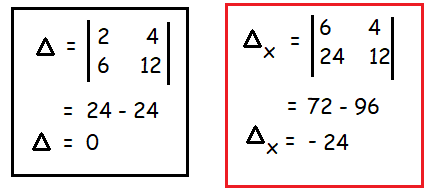
Here ∆ = 0 but ∆ₓ ≠ 0, then the system is consistent and it has no solution.

Example 6 :

Solve the  following equation using determinant method

2x+y  =  3 and 6x+3y  =  9

Solution :

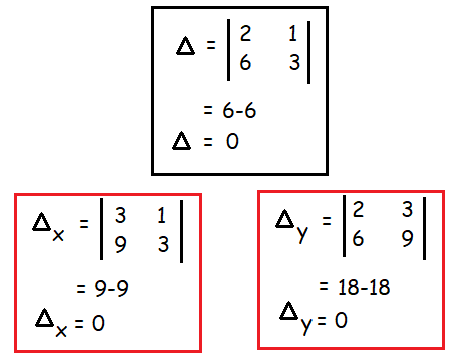
Since ∆ = 0, ∆ₓ = 0 and  ∆ᵧ = 0 and atleast one of the element in ∆ is non zero. Then the system is consistent and it has infinitely many solution. The above system is reduced into single equation. To solve this equation we have to assign y = k.

2x+y  =  3

2x+k  =  3

2x+k  =  3

2x  =  3-k

x  =  (3-k)/2

y  =  k

So, the solution is ((3-k)/2, k). Here k ∈ R where R is real numbers.

Example 7 :

Solve the following system of linear equation using Cramer’s rule

x + 2 y + 3 z = 6, 2x + 4 y + z = 7, 3x + 2 y + 9z = 14

Solution :

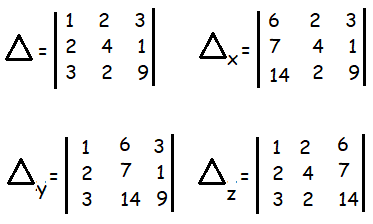
Δ = 1[36 - 2] - 2[18 - 3] + 3[4 - 12]

= 1(34) - 2(15) + 3(-8)

= 34 - 30 - 24

= 34 - 54

= -20

Δ_x = 6[36 - 2] - 2[63 - 14] + 3[14 - 56]

= 6[34] - 2[49] + 3[-42]

= 204 - 98 - 126

= 204 - 224

= -20

Δ_y = 1[63 - 14] - 6[18 - 3] + 3[28 - 21]

= 1[49] - 6[15] + 3[7]

= 49 - 90 + 21

= 70 - 90

= -20

Δ_z = 1[56 - 14] - 2[28 - 21] + 6[4 - 12]

= 1[42] - 2[7] + 6[-8]

= 42 - 14 - 48

= 42 - 62

= -20

x = Δ_x / Δ, y = Δ_y / Δ and z = Δ_z / Δ

x = -20/(-20), y = -20/(-20), z = -20/(-20)

x = 1, y = 1 and z = 1

Example 8 :

Solve the following system of linear equations using Cramer’s rule.

x + 2 y – z = 1, 3x + 8y + 2 z = 28, 4x + 9y + z = 14

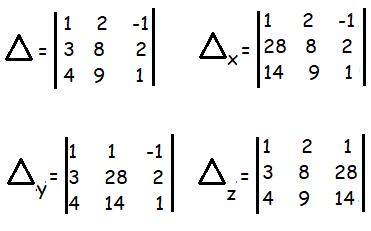
Δ = 1[8 - 18] - 2[3 - 8] - 1[27 - 32]

= 1(-10) - 2(-5) - 1(-5)

= -10 + 10 + 5

= 5

Δ_x = 1[8 - 18] - 2[28 - 28] - 1[252 - 112]

= 1(-10) - 2(0) - 1(140)

= -10 + 0 - 140

= -150

Δ_y = 1[28 - 28] - 1[3 - 8] - 1[42 - 112]

= 1(0) - 1(-5) - 1(-70)

= 0 + 5 - 70

= -65

Δ_z = 1[112 - 252] - 2[42-112] + 1[27 - 32]

= 1(-140) - 2(-70) + 1(-5)

= -140 + 140 - 5

= -5

x = Δ_x / Δ, y = Δ_y / Δ and z = Δ_z / Δ

x = -150/5, y = -65/5, z = -5/5

z = -30, y = -13, z = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.