DETERMINE IF a FUNCTION IS HOMOGENOUS AND FIND DEGREE
Let A = {(x, y) a < x < b, c < y < d} ∈ ℝ2, F : A-> ℝ, we say that F is a homogeneous function on A, if there exists a constant P such that F(λx, λy) = λp f(x, y) for all λ∈ℝ such that (λx, λy)∈A. This constant is called degree of F.
Step 1 :
In the given function, apply x = λx and y = λy.
Step 2 :
Do the possible simplification.
Step 3 :
Get the function in the form of λp f(x).
P is the degree of the polynomial.
Problem 1 :
In each of the following cases, determine whether the following function is homogeneous or not. If it is so, find the degree.
(i) f (x, y) = x2 y + 6x3+7
Solution :
Apply x = λx and y = λy
f (λx, λy) = (λx)2 (λy) + 6(λx)3+7
f (λx, λy) = λ2xy + 6λ3x3+7
We cannot factor λ from the function. So it is not a homogeneous function.
(ii)
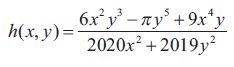
Solution :
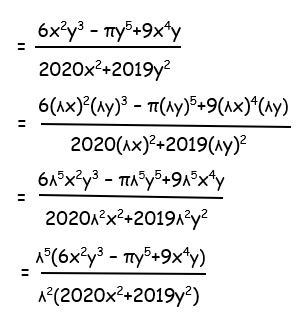
= λ3(6x2y3 – πy5+9x4y)/(2020x2+2019y2)
It is a homogenous function and its degree is 3.
(iii)
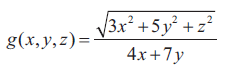
Solution :
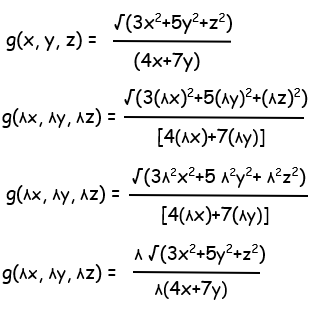
= λ0√(3x2+5y2+z2)/(4x+7y)
So, it is a homogenous function of degree 0.
(iv)
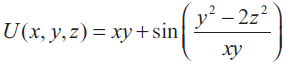
Solution :
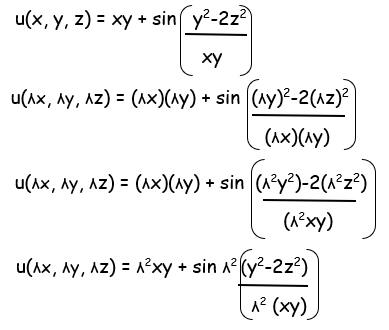
It is not a homogenous function.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 62)
Nov 05, 24 11:16 AM
Digital SAT Math Problems and Solutions (Part - 62) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 05, 24 11:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Worksheet on Proving Trigonometric Identities
Nov 02, 24 11:58 PM
Worksheet on Proving Trigonometric Identities
