DETERMINE IF A RELATION IS A FUNCTION

Let a ∈ A and b ∈ B, then the relation R from A to B can be defined as follows.

R  =  {(a, b)}

If this relation is a function, then it has to satisfy the following two conditions.  

(i) Every element of A has to be involved in mapping.

(ii) Every element of A has to be mapped to at most one element in B.   

In other words, 

(i) Every element  of A must have an image in B.

(ii) Every element of A must have only one image in B. 

If either of the above conditions is not met, then the relation is not a function.

There fore, 

All the functions are relations. But all the relations need not be functions.

If a relation has to be a function, it has to meet the above two conditions. 

Solved Examples

Example 1 :

Check whether the following relation is a function or not. 

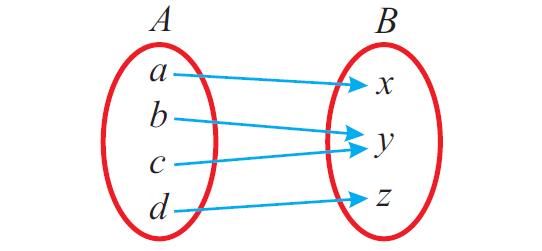
In the above mapping from A to B, every element of A has an image in B. And also, every element of A has only one image in B.

Since the above relation meets both the conditions, it is a function. 

Example 2 :

Check whether the following relation is a function or not. 

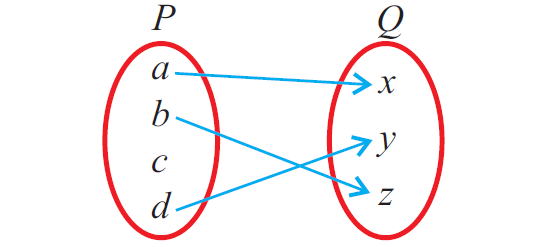
In the above mapping from P to Q, the element 'c' in P does not have image in Q. 

Since the above relation does not meet the first condition, it is not a function.

Example 3 :

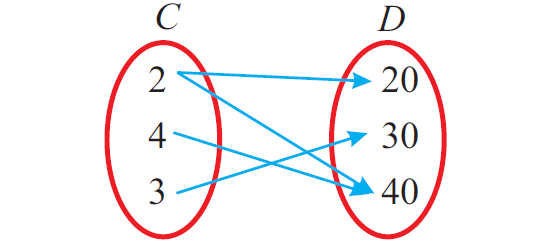
In the above mapping from C to D, every element of C has an image in D. 

But, the element '2' in C has two images (20 and 40) in D. Since the above relation does not meet the second condition, it is not a function.

Vertical Line Test

Key Concept :

A graph represents a function only if every vertical line intersects the graph in at most one point.

Example 1 : 

Use the vertical line test to determine whether the following graph represents a function.

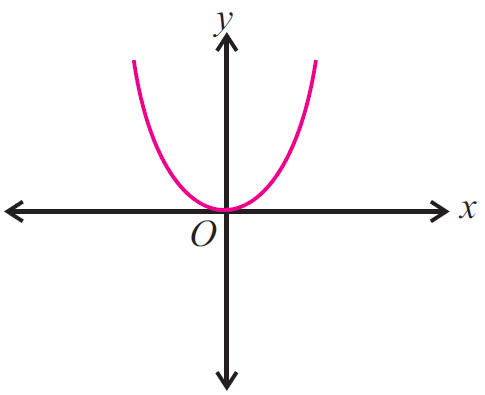
Solution :

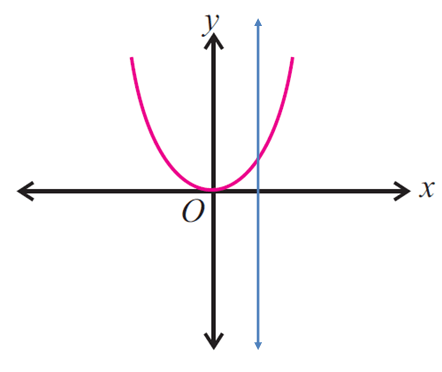
Since the vertical line intersects the graph in at most one point, the given  graph represents a function. 

Example 2 : 

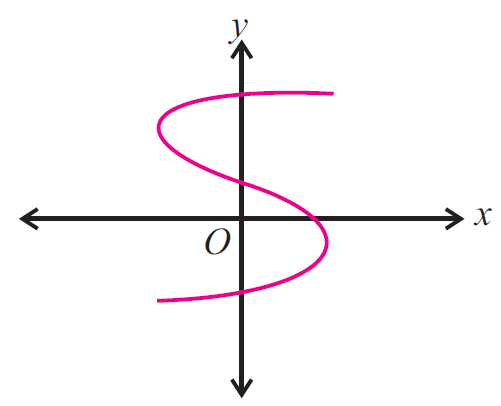
Use the vertical line test to determine whether the following graph represents a function.

Solution :

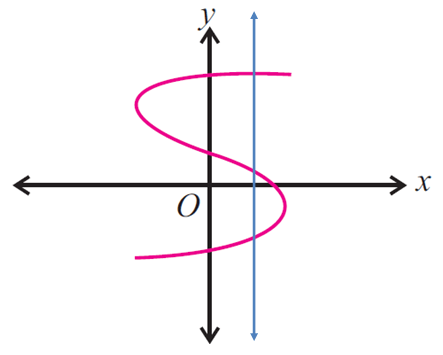
Since the vertical line intersects the graph in more than one point (three points), the given  graph does not represent a function. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.