DETERMINE IF THE RELATIONSHIP IS PROPORTIONAL

Direct Proportion :

If 'y' is directly proportional to 'x', then

y = kx

where 'k' is the constant of proportionality.

Inverse Proportion :

If 'y' is inversely proportional to 'x', then

y = k/x

where 'k' is the constant of proportionality.

How to determine if the relationship is proportional

If two different quantities are given, how to check whether the relationship between them is proportional? 

We have to get ratio of the two quantities for all the given values.

If all the ratios are equal, then the relationship is proportional.

If all the ratios are not equal, then the relationship is not proportional.

Determining Proportional Relationships

Example 1 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

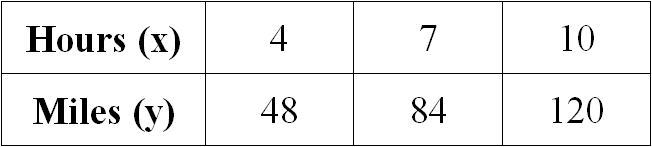
Solution :

Let us get the ratio of x and y for all the given values.

4/48 = 1/12

7/84 = 1/12

10/120 = 1/12

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 4 and y = 48.

48 = k(4)

12 = k

So, the constant of proportionality is 12.

Example 2 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

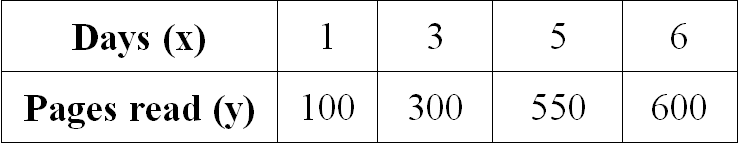
Solution :

Let us get the ratio of x and y for all the given values.

1/100 = 1/100

3/300 = 1/100

5/550 = 1/110

6/600 = 1/100

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 3 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

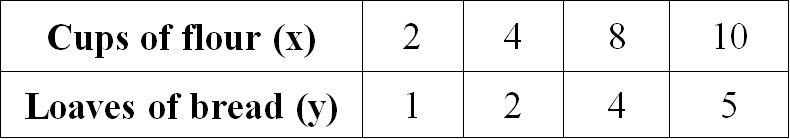
Solution :

Let us get the ratio of x and y for all the given values.

2/1 = 2

4/2 = 2

8/4 = 2

10/5 = 2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 2 and y = 1.

1 = k(2)

1/2 = k

So, the constant of proportionality is 1/2.

Example 4 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

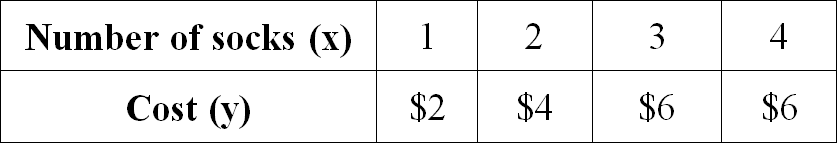
Solution :

Let us get the ratio of x and y for all the given values. 

1/2 = 1/2

2/4 = 1/2

3/6 = 1/2

4/6 = 2/3

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 5 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

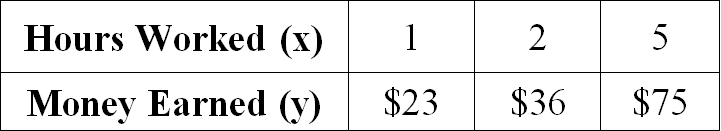
Solution :

Let us get the ratio of x and y for all the given values.

1/23 = 1/23

2/36 = 1/18

5/75 = 1/15

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 6 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

Solution :

Let us get the ratio of x and y for all the given values. 

2/4 = 1/2

4/8 = 1/2

6/12 = 1/2

8/16 = 1/2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 2 and y = 4.

4 = k(2)

2 = k

So, the constant of proportionality is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.