DETERMINING IF A TRIANGLE IS A RIGHT TRIANGLE

In each case, determine if the side lengths lengths form a right triangle.

Example 1 :

20, 21, 29

Solution :

Let a = 20, b = 21 and c = 29.

c² = 29²

= 841 ----(1)

a² + b² = 20² + 21²

= 400 + 441

= 841 ----(2)

From (1) and (2), 

c² = a² + b²

The side lengths 20, 21 and 29 form a right triangle. 

Example 2 :

8, 10, 12

Solution :

Let a = 8, b = 10 and c = 12.

c² = 12²

= 144 ----(1)

a² + b² = 8² + 10²

= 64 + 100

= 164 ----(2)

From (1) and (2),

c² ≠ a² + b²

The side lengths 8, 10 and 12 do not form a right triangle. 

Example 3 :

30, 40, 50

Solution :

Let a = 30, b = 40 and c = 50.

c² = 50²

= 2500 ----(1)

a² + b² = 30² + 40²

= 900 + 1600

= 2500 ----(2)

From (1) and (2),

c² = a² + b²

The side lengths 30, 40 and 50 form a right triangle.

Example 4 :

6, 12, 18

Solution :

Let a = 6, b = 12 and c = 18.

c² = 18²

= 324 ----(1)

a² + b² = 6² + 12²

= 36 + 144

= 180 ----(2)

From (1) and (2),

c² ≠ a² + b²

The side lengths 6, 12 and 18 do not form a right triangle. 

Example 5 :

24, 30, 36

Solution :

Let a = 24, b = 30 and c = 36.

c² = 36²

= 1296 ----(1)

a² + b² = 24² + 30²

= 576 + 900

= 1476 ----(2)

From (1) and (2),

c² ≠ a² + b²

The side lengths 24, 30 and 36 do not form a right triangle.

Example 6 :

A triangle can have _________ right angle.

Solution :

A triangle can have one right angle.

Example 7 : 

Each angle of an acute angled triangle is ________than 90⁰

Solution :

Each angle of an acute angled triangle is lesser than 90⁰

Example 8 :

The sum of the two acute angles in a right angled triangle is __

Solution :

The sum of the two acute angles in a right angled triangle is 90⁰

Example 9 :

The triangle DEF is shown below. Find the length of EF to 1 decimal place.

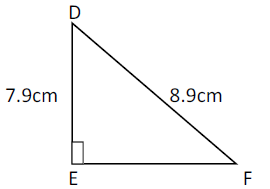
Solution :

Since the triangle DEF is a right triangle, it must satisfy the Pythagorean theorem.

c² = a² + b²

DF² = DE² + EF²

(8.9)² = 7.9² + EF²

79.21 = 62.41 + EF²

EF² = 79.21 - 62.41

EF² = 16.8

EF = √16.8

EF = 4.09 cm

Approximately 4.1 cm

Example 10 :

To wash a window that is 8 meters off the ground, Ben leans a 10 meter ladder against the side of the building. To reach the window, how far from the building should Ben place the base of the ladder?

Solution :

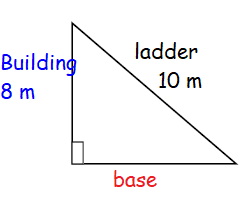
Let x be the distance between base of the building to the foot of the ladder.

10² = 8² + x²

100 = 64 + x²

x² = 100 - 64

x² = 36

x = √36

x = 6 m

So, the distance between base of the building to the foot of the ladder is 6 m.

Example 11 :

A rectangular swimming pool is 21 meters wide and 50 metres long. Calculate the length of the diagonal to 1 decimal place.

Solution :

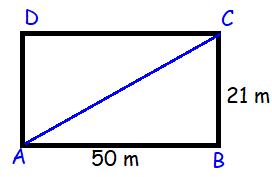
AC² = AB² + BC²

AC² = 50² + 21²

= 2500 + 441

= 2941

AC = √2941

AC = 54.23

So, the length of diagonal is 54.23 m

Example 12 :

Miss Barker is teaching a 5th grade class. She is standing 12 feet in front of Jim. Francisco is sitting 5 feet to Jim’s right. How far apart are Miss Barker and Francisco?

Solution :

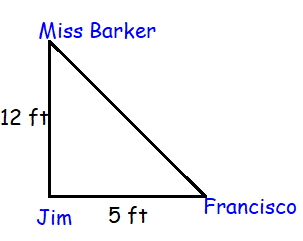
Let x be the distance between Miss Barker and Francisco.

x² = 12² + 5²

x² = 144 + 25

x² = 169

x = √169

x = 13 ft

So, the distance between Miss Barker and Francisco is 13 ft.

Example 13 :

A triangle has sides with lengths of 10 metres, 16 metres and 20 metres. Is it a right angled triangle? Explain your reasoning.

Solution :

Let a = 10 m, b = 16 m and c = 20 m

c² = a² + b²

20² = 10² + 16²

400 = 100 + 256

400 ≠ 356

So, the given sides are not measures of the right triangle.

Example 14 :

a) One side of a right angled triangle is 10 cm. The other two are both of length x. Calculate x to 2 decimal places.

b) Find the perimeter of the triangle in part a)

Solution :

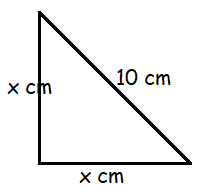
a)  10² = x² + x²

100 = 2x²

x² = 100/2

x² = 50

x = √50

x = 7.07

b) Perimeter of the triangle = x + x + 10

= 7.07 + 7.07 + 10

= 24.14 cm

So, the required length of diagonal is 24.14 cm

Example 15 :

Find the length of the diagonal of a square of side 4 cm to 2 decimal places.

Solution :

In square all sides will be equal. Let x be the length of diagonal.

x² = 4² + 4²

x² = 16 + 16

x² = 32

x = √32

x = 5.65

So, the required length of diagonal is 5.65 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.