DETERMINING RATE OF CHANGE AND INITIAL VALUE

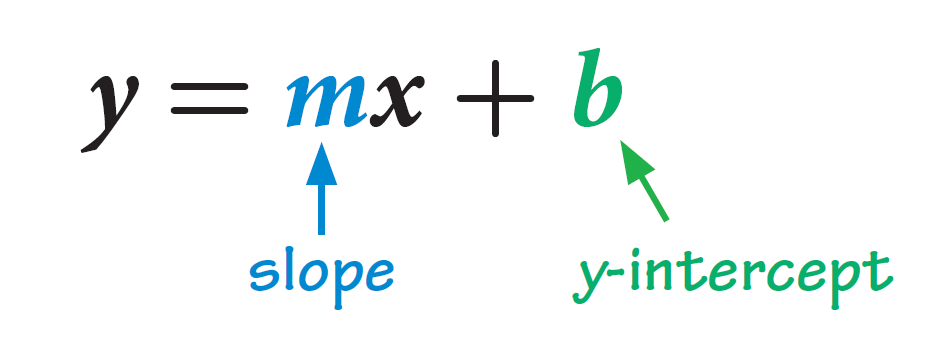
The linear equation shown is written in the slope-intercept form of an equation. Its graph is a line with slope m and y-intercept b.

A linear relationship has a constant rate of change. You can find the rate of change m and the initial value b for a linear situation from a table of values.

Example 1 :

Find the slope and y-intercept of the line represented by the table. And also find the equation of the line in slope-intercept form.

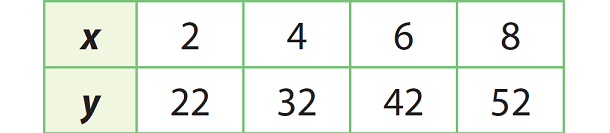
Solution :

Step 1 : 

Confirm that the rate of change is constant.

Change in y-value / change in x-value :

=  (32 - 22)/(4 - 2) = 10/2 = 5

=  (42 - 32)/(6 - 4) = 10/2 = 5

=  (52 - 42)/(8 - 6) = 10/2 = 5

The rate of change is a constant and it is 5.

So, the slope is 5.

Step 2 :

Find the initial value y. That is, the value of y when x  = 0. 

Work backward from x = 2 to x = 0 to find the initial value.

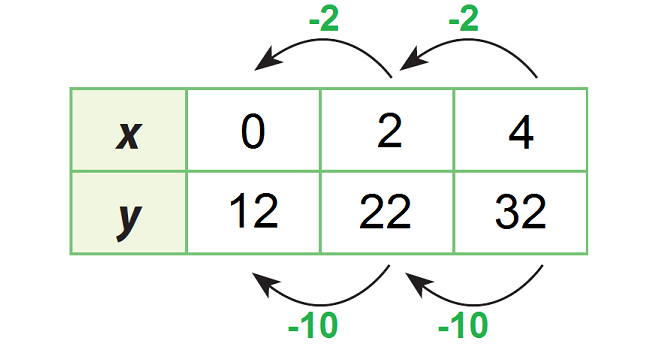
The initial value is 12. That is, y-intercept is 12. 

So, the equation of the line is 

y  =  5x + 12

Example 2 :

A phone salesperson is paid a minimum weekly salary and a commission for each phone sold, as shown below. Confirm that the relationship is linear and give the constant rate of change and the initial value.

Solution :

Step 1 : 

Confirm that the rate of change is constant.

Phones Sold (10 to 20) :

Change in income/Change in phones sold is

=  (630 - 480)/(20 - 10)

=  150/10

=  15

Phones Sold (20 to 30) :

Change in income/Change in phones sold is

=  (780 - 630)/(30 - 20)

=  150/10

=  15

Phones Sold (30 to 40) :

Change in income/Change in phones sold is

=  (930 - 780)/(40 - 30)

=  150/10

=  15

The rate of change is a constant and it is 15.

The salesperson receives a $15 commission for each phone sold.

Step 2 :

Find the initial value when the number of phones sold is 0.

Work backward from x = 10 to x = 0 to find the initial value.

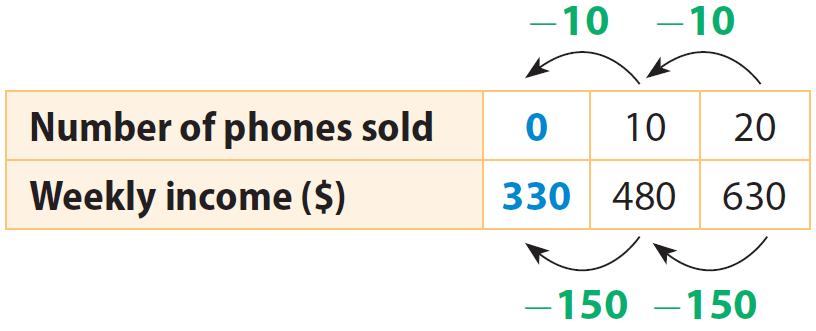
The initial value is $330. The salesperson receives a salary of $330 each week before commissions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.