DIFFERENTIABILITY AND CONTINUITY WORKSHEET

(1)  Find the derivatives of the following functions using first principle.

(i) f(x)  =  6       Solution

(ii)  f(x)  =  -4x + 7       Solution

(iii)  f(x)  =  -x² + 2        Solution

(2)  Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

(i)  f(x)  =  |x - 1|       Solution

(ii)  f(x)  =  √(1 - x²)       Solution

Solution

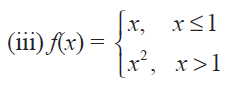
(3)  Determine whether the following function is differentiable at the indicated values.

(i) f(x) = x | x | at x = 0        Solution

(ii)  f(x) = |x² - 1| at x = 1      Solution

(iii)  f(x) = |x| + |x - 1| at x = 0, 1       Solution

(iv)  f(x)  =  sin |x| at x = 0        Solution

(4)  Show that the following functions are not differentiable at the indicated value of x.

(i)

Solution

Solution

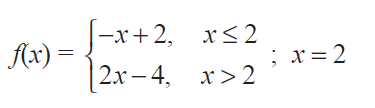
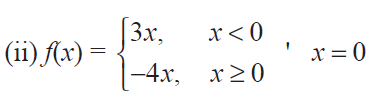
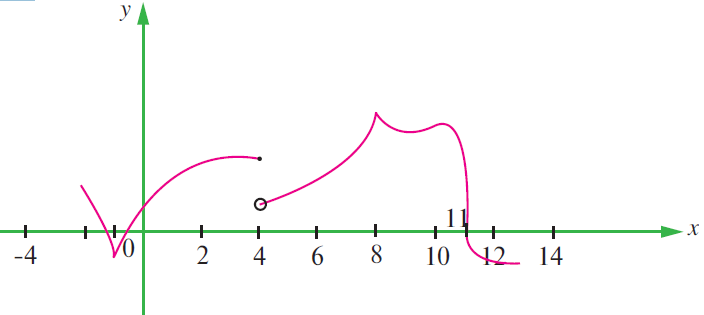
(5)  The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.

Solution

(6)  If f(x) = |x + 100| + x², test whether f'(-100) exists.

Solution

(7)  Examine the differentiability of functions in R by drawing the diagrams.

(i) | sin x |            Solution

(ii)  |cos x|          Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.