DIFFERENTIATION FORMULAS

Differentiation formulas :

Here we are going to see list of formulas used in differentiation.

Differentiation using first principles : 

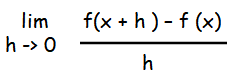
Formulas in limits :

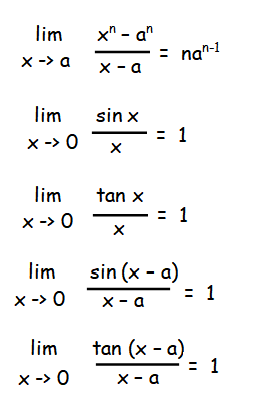
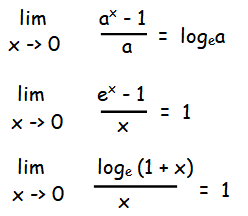
Example 1 :

Differentiate x⁵ tan x

Solution:

Let y = x⁵ tan x

 u = x⁵         v = tan x

 u' = 5x⁴       v' = sec² x  

(UV)' = UV' + VU'

  =  (x⁵)sec² x  + (tan x)(5x⁴)

  =  x⁵sec² x  + 5x⁴tan x         

  =  x⁴[xsec² x  + tan x]

Example 2 :

Differentiate (x² - 1)/ (x² + 1) with respect to x

Solution :

let y = (x² - 1)/ (x² + 1)

 u = x² - 1                  v = x² + 1

 u' = 2x - 0                 v' = 2x + 0

 u' = 2x                      v' = 2x         

So    y' = [(x² + 1) (2x) - (x² - 1)(2x)] /(x² + 1)²

  =  [(2x)(x² + 1)  - (2x)(x² - 1)] /(x² + 1)²

  =  [(2x³ + 2x)  - (2x³ - 2x)] /(x² + 1)²

  =  [2x³ + 2x  - 2x³ + 2x] /(x² + 1)²

  =  4x /(x² + 1)²

Example 3 :

Differentiate log (sin x) with respect to x

Solution :

 let y = log (sin x) and we are going to take u = sin X

Now the function becomes y = log u 

dy/dx = (dy/du) x (du/dx)

 dy/du = 1/u 

 du/dx = cos X

 dy/dx = (1/u)   x cos X

=  cos X/u

=  cos X/sin X

=   cot X 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.