DIFFICULT PROBLEMS ON GEOMETRIC SERIES

Problem 1 :

Kumar writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with the instruction that they continue the process similarly. Assuming that the process is unaltered and it costs 2 to mail one letter, find the amount spent on postage when 8th set of letters is mailed.

Solution :

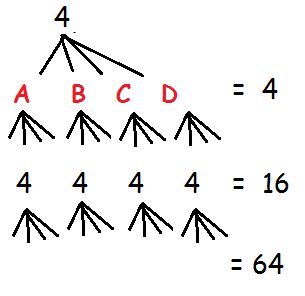
By writing the number of letters as series, we get

  4  + 16 + 64 + ...................

It forms a geometric series. Now we have to find the sum of the series upto 8 terms.

S_n  =  a(rⁿ - 1)/(r - 1)

n = 8, a = 4 and r = 16/4  =  4

S₈  =  4(4⁸ - 1)/(4 - 1)

  =  4(65535)/3

  =  4(21845)

  =  87380

So far, we get the number of letters posted. Amount spend for one post is 2.

Required cost  =  2 (87380)

=  174760

Problem 2 :

Find the rational form of the number 

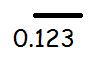
Solution :

x = 0.123 123 123.............  ------(1)

Multiply each side by 1000, we get

1000x  =  123.123 123.............. ------(2)

(2) - (1)

1000x - x  =  123.123 123.............. - 0.123 123 123..............

999x  =  123

x  =  123/999

x  =  41/333

Hence the rational form of the given number is 41/333.

Problem 3 :

If Sn  =  (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + ......  n terms then prove that

(x - y) S_n  =  {[x²(xⁿ - 1)/(x - 1)] - [y²(yⁿ - 1)/(y - 1)]}

Solution :

=  (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + ......  n

Multiply and divide it by (x - y)

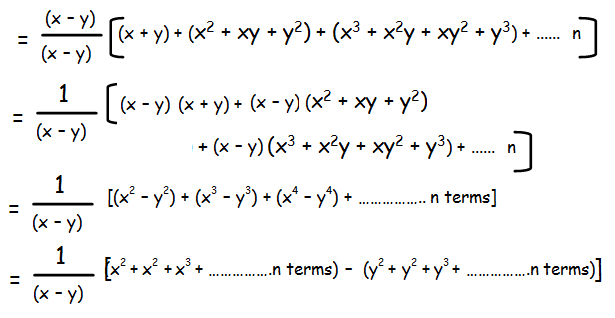
[x² + x³ + x⁴ + ................n terms]  ----(1)

S_n  =  [x² (xⁿ - 1)/(x - 1)]

[y² + y³ + y⁴ + ................n terms]  ----(1)

S_n  =  [y² (yⁿ - 1)/(y - 1)]

  =  1/(x -y){[x²(xⁿ-1)/(x-1)] - [y²(yⁿ - 1)/(y - 1)]}

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.