DILATIONS WORKSHEET

Problem 1 :

Identify the dilation and find its scale factor.

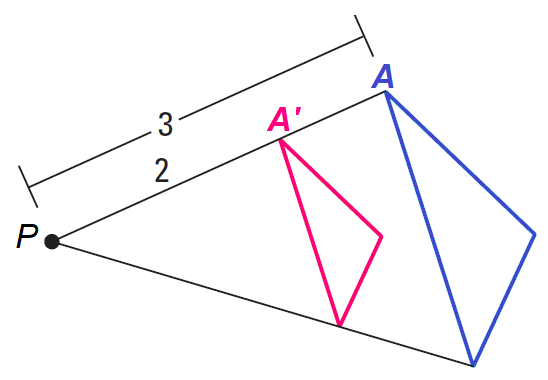
Problem 2 :

Identify the dilation and find its scale factor.

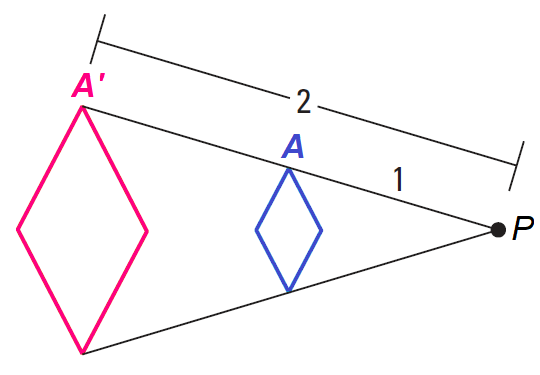
Problem 3 :

Draw a dilation of rectangle ABCD with

A(2, 2), B(6, 2), C(6, 4) and D(2, 4)

Use the origin as the center and use a scale factor of 1/2. How does the perimeter of the preimage compare to the perimeter of the image ?

Problem 4 :

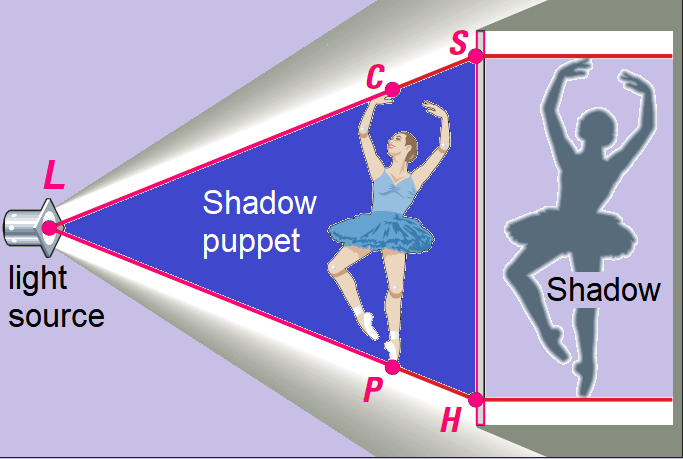
Shadow puppets have been used in many countries for hundreds of years. A flat figure is held between a light and a screen. The audience on the other side of the screen sees the puppet’s shadow. The shadow is a dilation, or enlargement, of the shadow puppet. When looking at a cross sectional view, 

ΔLCP ∼ ΔLSH

The shadow puppet shown below is 12 inches tall (CP in the diagram). Find the height of the shadow, SH, for each distance from the screen. In each case, by what percent is the shadow larger than the puppet ?

a. LC  =  LP  =  59 in. ; LS  =  LH  =  74 in.

b. LC  =  LP  =  66 in. ; LS  =  LH  =  74 in.

1. Answer :

Because PA'/PA = 2/3, the scale factor is 2/3.

Because the scale factor 2/3 is less than 1, this is a reduction.

2. Answer :

Because PA'/PA = 2/1, the scale factor is 2.

Because the scale factor 2 is greater than 1, this is an enlargement.

3. Answer :

Because the center of the dilation is the origin, we can find the image of each vertex by multiplying its coordinates by the scale factor 1/2.

P(2, 2) ----> P'(1, 1)

Q(6, 2) ----> Q'(3, 1)

R(6, 4) ----> R'(3, 2)

S(2, 4) ----> S'(1, 2)

Let us plot the above points in xy-plane.

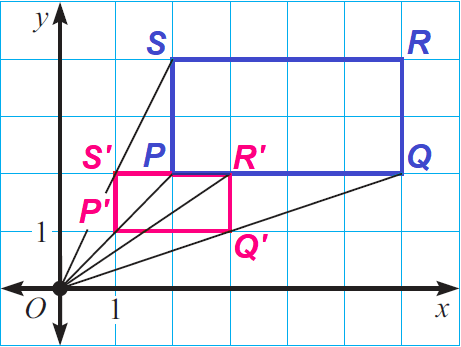
From the graph, we can see that the preimage has a perimeter of 12 and the image has a perimeter of 6. A preimage and its image after a dilation are similar figures. Therefore, the ratio of the perimeters of a preimage and its image is equal to the scale factor of the dilation.

4. Answer :

Part (a) :

59/74 = 12/SH

By reciprocal property of proportion, 

74/59 = SH/12

SH/12 = 74/59

Multiply each side by 12.

12 ⋅ (SH/12) = (74/59) ⋅ 12

SH ≈ 15

To find the percent of size increase, use the scale factor of the dilation.

Scale factor = SH/CP

= 15/12

= 1.25

So, the shadow is 25% larger than the puppet.

Part (b) :

66/74 = 12/SH

By reciprocal property of proportion,

74/66 = SH/12

SH/12 = 74/66

Multiply each side by 12.

12 ⋅ (SH/12) = (74/66) ⋅ 12

SH ≈ 13.45

To find the percent of size increase, use the scale factor of the dilation.

Scale factor = SH/CP

= 13.45/12

= 1.12

So, the shadow is 12% larger than the puppet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.