DIRECT VARIATION AND INVERSE VARIATION

Direct Variation

Please look at the following situations.

You buy more pens ---> Costs you more

More no. of students ---> More no. of teachers

Travel less distance ---> Time taken is less

No. of books reduced ---> Weight of bag is less

Thus we can say, if an increase in one quantity produces a proportionate increase in another quantity, then the quantities are said to be in direct variation.

or

If a decrease in one quantity produces a proportionate  decrease in another quantity, then the quantities are said to be in direct variation.

Change in both the quantities must be same.

That is,

Increase ----> Increase

or

Decrease ----> Decrease

Inverse Variation

Please look at the following situations.

More men ----> Less days to complete a work

More speed ----> Less time to cover the distance

More vehicles on the road ----> Less road space

Less time per day ----> More days to complete the work

Thus we can say, if an increase in one quantity produces a proportionate decrease in another quantity, then the quantities are said to be in inverse variation.

or

If a decrease in one quantity produces a proportionate increase in another quantity, then the quantities are said to be in inverse variation.

Changes in the quantities must be opposite.

That is,

Increase -----> Decrease

or

Decrease -----> Increase

Shortcuts

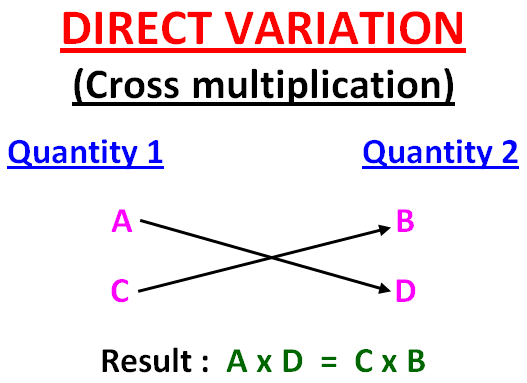
Solved Problems

Problem 1 :

75 basketballs cost $1143.75. Find the cost of 26 basketballs.

Solution :

This is a situation of direct variation.

Because,

less number of basket balls ----> cost will be less

Let m be the cost of 26 basket balls.

Since this is direct variation, we have to apply the shortcut cross multiplication.

75m  =  26(1143.75)

m  =  (29737.5)/75

m  =  $396.50

Problem 2 :

7 men can complete a work in 52 days. In how many days will 13 men finish the same work?

Solution :

This is a situation of inverse variation.

Because,

more men ----> less days

Let m be the required no. of days.

Since this is inverse variation, we have to apply the shortcut straight multiplication.

7(52) = 13m

364/13 = m

m = 28 days

Problem 3 :

A book contains 120 pages and each page has 35 lines. How many pages will the book contain if every page has 24 lines per page ?

Solution :

This is a situation of inverse variation.

Because,

less lines ----> more pages

Let m be the required number of pages.

Since this is inverse variation, we have to apply the shortcut straight multiplication.

120(35) = m(24)

(4200)/24 = m

m = 175 pages.

Problem 4 :

A truck covers a particular distance in 3 hours with the speed of 60 miles per hour. If the speed is increased by 30 miles per hour, find the time taken by the truck to cover the same distance

Solution :

This is a situation of inverse variation.

Because,

more speed ----> less time

If the given speed 60 mph is increased by 30 mph,

then the new speed  =  90 mph

Let m be the required time.

Since this is inverse variation, we have to apply the shortcut straight multiplication.

3(60) = m(90)

180/90 = m

m = 2 hrs

Problem 5 :

In a business, if A can earn $7500 in 2.5 years, At the same rate, find his earning for 4 years.

Solution :

This is a situation of direct variation.

Because,

more time ----> more earning

Since this is direct variation, we have to apply the shortcut cross multiplication

2.5m = 4(7500)

m = (30000)/2.5

m = $12000

So, the earning for 4 years is $12000.

Problem 6 :

In 36.5 weeks, Miguel raised $2,372.50 for cancer research. How much money will he raise 20 weeks ?

Solution :

This is a situation of direct variation.

Because,

less number of weeks ----> amount raised will be less

Let m be the required amount of money.

Since this is direct variation, we have to apply the shortcut cross multiplication.

36.5m = 20(2372.50)

m = (47450)/36.5

m = $1300

Problem 7 :

Alex  takes 15 days to reduce 30 kilograms of his weight by doing 30 minutes exercise per day. If he does exercise for 1 hour 30 minutes per day, how many days will he take to reduce the same weight ?

Solution :

This is a situation of inverse variation.

Because,

more minutes per day----> less days to reduce the weight

And also

1 hour 30 minutes per day  =  90 minutes per day

Let m be the required number of days.

Since this is inverse variation, we have to apply the shortcut straight multiplication

15(30) = m(90)

450/90 = m

m = 5 days

Problem 8 :

If 5 men can paint a house in 18 hours, how many men will be able to paint it in 10 hours ?

Solution :

This is a situation of inverse variation.

Because,

less hours  ----> more men

Let m be the required number of men.

Since this is inverse variation, we have to apply the shortcut straight multiplication.

5(18) = m(10)

90/10 = m

m = 9 men

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.