DIRECTION COSINES AND RATIOS

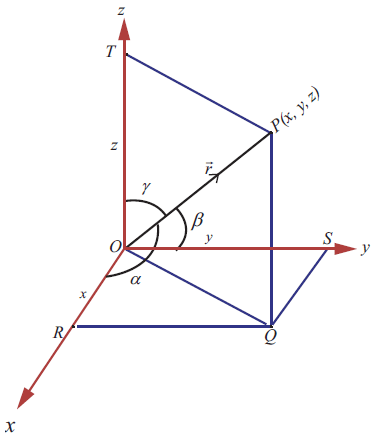
Let P be a point in the space with coordinates (x, y, z) and of distance r from the origin. 

Let R, S and T be the foots of the perpendiculars drawn from P to the x, y and z axes respectively. Then

∠PRO  =  90°

∠PSO  =  90°

∠PTO  =  90° 

OR = x, OS = y, OT = z and OP = r.

OR = x, OS = y, OT = z and OP = r.

(It may be difficult to visualize that ∠PRO  =  ∠PSO  =  ∠PTO  =  90° in the figure; as they are foot of the perpendiculars to the axes from P; in a three dimensional model we can easily visualize the fact.)

Let α, β, γ be the angles made by the vector OP vector with the positive x, y and z axes respectively. That is,

∠PRO   =  α, ∠POS   =  β, ∠POT   =  γ

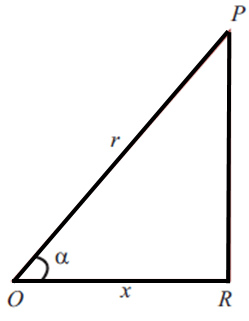In triangle OPR, ∠PRO = 90°, ∠POR =  α, OR = x, and OP = r. Hence cos α = OR/OP  =  x/r

In a similar way we can find that cos β  =  y/r and cos γ  =  z/r .

Direction Angles :

Here the angles α, β, γ are called direction angles of the vector OP vector = r vector.

Direction Cosines :

Cos α, cos β, cos γ are called direction cosines of the vector OP = xi vector + yj vector + zk vector.

Thus (x/r, y/r, z/r), where r  =  √(x² + y² + z²) are the direction cosines of the vector r vector  =  xi vector + yj vector + zk vector.

How to verify the direction ratios are direction cosines of a vector ?

Question 1 :

Verify whether the following ratios are direction cosines of some vector or not.

(i) 1/5 , 3/5 , 4/5

Solution :

In order to verify the given ratios are direction cosines, it has to satisfy the condition given below.

The sum of the squares of the direction cosines of r vector is 1.

That is , 

x² + y² + z²  =  1

r vector = xi vector + yj vector + zk vector 

r vector = (1/5)i vector + (3/5)j vector + (4/5)k vector 

x² + y² + z²  =  (1/5)² + (3/5)² + (4/5)²

   =  (1/25) + (9/25) + (16/25)

  =  (1 + 9 + 16)/25

  =  26/25 

x² + y² + z²  ≠ 1

Hence the direction ratios are not direction cosines of some vector.

(ii) 1/√2, 1/2 , 1/2

Solution :

r vector = (1/√2)i vector + (1/2)j vector + (1/2)k vector 

x² + y² + z²  =  (1/√2)² + (1/2)² + (1/2)²

   =  (1/2) + (1/4) + (1/4)

  =  (2 + 1 + 1)/4

  =  1

Hence the direction ratios are the direction cosines of some vector.

(iii) 4/3, 0, 3/4

Solution :

r vector = (4/3)i vector + (0)j vector + (3/4)k vector 

x² + y² + z²  =  (4/3)² + (0)² + (3/4)²

   =  (16/9) + 0 + (9/16)

  =  (256 + 0 + 81)/144

x² + y² + z²  ≠ 1

Hence the direction ratios are not direction cosines of some vector.

Question 2 :

Find a direction ratio and direction cosines of the following vectors.

(i) 3i vector + 4j vector - 6k vector

(ii)  3i vector - 4k vector

Solution :

(i) 3i vector + 4j vector - 6k vector

Let a vector = 3i vector + 4j vector - 6k vector

The direction ratios of a vector is 3, 4 and -6

Directions cosines are x/r, y/r and x/r

r = √x² + y² + z²

r = √3² + 4² + (-6)²

= √(9 + 16 + 36)

= √61

Direction cosines are 3/√61, 4/√61 and -6/√61

(ii)  3i vector - 4k vector

Let a vector = 3i vector - 4k vector

The direction ratios of a vector is 3, 0 and -4

Directions cosines are x/r, y/r and x/r

r = √x² + y² + z²

r = √3² + 0² + (-4)²

= √(9 + 0 + 16)

= √25

r = 5

Direction cosines are 3/5, 0 and -4/5.

Question 3 :

(i) Find the direction cosines of a vector whose direction ratios are 2, 3, - 6.

(ii) Can a vector have direction angles 30°, 45°, 60° ?

(iii) Find the direction cosines of AB vector where A is (2, 3, 1) and B is (3, - 1, 2).

(iv) Find the direction cosines of the line joining (2, 3, 1) and (3, - 1, 2).

(v) The direction ratios of a vector are 2, 3, 6 and it’s magnitude is 5. Find the vector.

Solution :

(i) Direction ratios are 2, 3, - 6

r = √x² + y² + z²

r = √2² + 3² + (-6)²

= √(4 + 9 + 36)

= √49

= 7

Direction cosines are 2/7, 3/7 and -6/7.

(ii) Direction angles are 30°, 45°, 60°

cos²α + cos²β + cos²Γ = 1

Here α = 30, β = 45 and Γ = 60

3/4 + 1/2 + 1/4 ≠ 1

(3 + 2 + 1)/4 ≠ 1

6/4 ≠ 1

Therefore they are not direction angles of any vector.

(iii) OA vector = 2i vector + 3j vector + 1k vector

OB vector = 3i vector - 1j vector + 2k vector

AB vector = OB vector - OA vector

= (3i vector - 1j vector + 2k vector) - (2i vector + 3j vector + 1k vector)

= (3i vector - 2i vector) + (-1j vector - 3j vector) + (2k vector - 1k vector)

= 1i vector - 4j vector + 1k vector

r = √x² + y² + z²

r = √1² + (-4)² + 1²

= √(1 + 16 + 1)

= √18

Direction cosines are 1/√18, -4/√18 and 1/√18.

(iv) But any point can be taken as first point. Hence we have another set of direction cosines with opposite direction. Thus, we have another set of direction ratios

-1/√18, 4/√18, -1/√18

(v) The direction ratios are 2, 3, 6

r = √2² + 3² + 6²

= √(4 + 9 + 36)

= √49

= 7

5/7 (2i vector + 3j vector + 6k vector)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.