DISTANCE AND AREA IN THE COORDINATE PLANE

We can solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane.

We can use coordinates to find the area of a figure and and absolute value to find distances between points with the same first coordinate or the same second coordinate.

Examples

Example 1 :

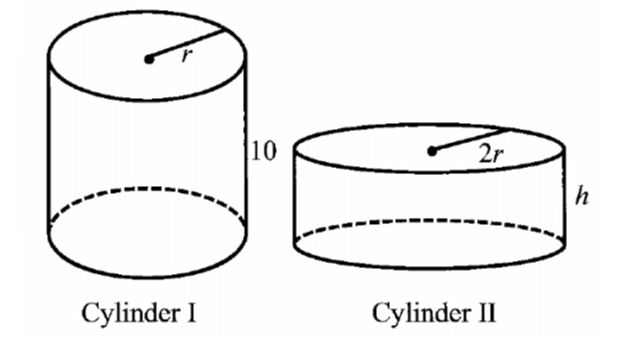
Find the distance between points A and B in the graph given below. 

Solution :

From the graph, the ordered pair  of A is (3, 3) and B is (3, -4)

Since, the distance is parallel to "y" axis, let us take the "y" coordinates in the two points A and B. 

They are 3 and -4. 

To find the distance between the two points , we have to add the absolute values of the y-coordinates

Then, the distance between the two points A and B is

=  |3| + |-4|

=  3 + 4

=  7

So, the distance between points A and B is 7 units.

Example 2 :

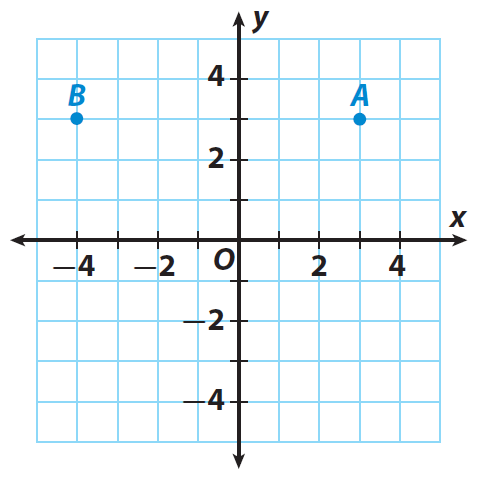
Find the distance between points A and B in the graph given below. 

Solution :

From the graph, the ordered pair  of A is (3, 3) and B is (-4, 3)

Since, the distance is parallel to "x" axis, let us take the "x" coordinates in the two points A and B. 

They are 3 and -4. 

To find the distance between the two points , we have to add the absolute values of the x-coordinates

Then, the distance between the two points A and B is

=  |3| + |-4|

=  3 + 4

=  7

So, the distance between points A and B is 7 units.

Example 2 :

What type of polygon can you make by plotting these points ?

Point A (-4, 2)

Point B (2, 2)

Point C (-4, -2)

Point D (2, -2)

And also find the area of the polygon made by these points. 

Solution : 

To know the type of the polygon, let us plot the given points on the coordinate plane. 

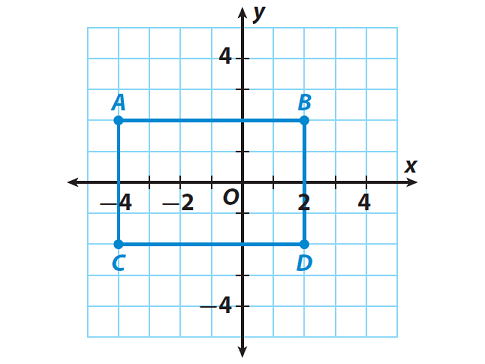
When we plot the given points on the coordinate plane, it is clear that the polygon we get is rectangle. 

Here, AB represents the length  and AC represents the width of the rectangle ABCD.

To find the area of the rectangle, we have to find the length AB and width  AC. 

Finding the length AB : 

From the graph, the ordered pair  of A is (-4, 2) and B is (2, 2)

Since, the distance is parallel to "x" axis, let us take the "x" coordinates in the two points A and B. 

They are -4 and 2. 

To find the distance between the two points , we have to add the absolute values of the x-coordinates

Then, the distance between the two points A and B is

=  |-4| + |2|

=  4 + 2

=  6

Therefore, the length AB is 6 units. 

Finding the width AC :

From the graph, the ordered pair of A is (-4, 2) and B is (-4, -2)

Since, the distance is parallel to "y" axis, let us take the "y" coordinates in the two points A and B. 

They are 2 and -2. 

To find the distance between the two points , we have to add the absolute values of the y-coordinates

Then, the distance between the two points A and B is

=  |2| + |-2|

=  2 + 2

=  4

Therefore, the width AB is 4 units.

Finding area of the rectangle ABCD :

Area of the rectangle ABCD is

=  length x width

=  6 x 4

=  24 

So, the area of the rectangle ABCD is 24 square units. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.