DISTANCE BETWEEN TWO POINTS
Let P(x1, y1) and Q(x2, y2) be two points in the Cartesian plane (or xy –plane), at a distance ‘d’ apart.
That is
d = PQ
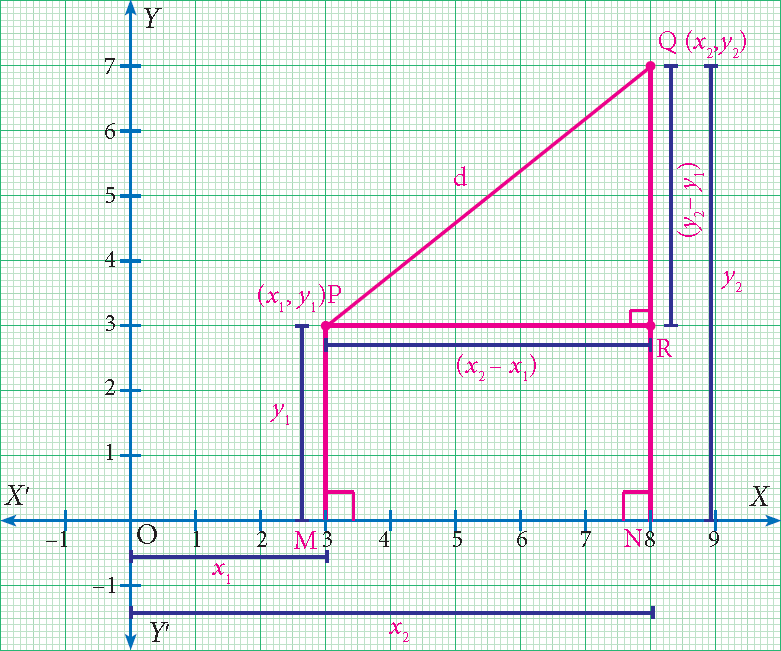
By the definition of coordinates,
|
OM = x1 ON = x2 |
MP = y1 NQ = y2 |
Step 1 :
Now, (PR ⊥ NQ)
PR = MN
(Opposite sides of the rectangle MNRP)
Step 2 :
Find the length of MN.
MN = ON - OM
MN = x2 - x1
Step 3 :
Find the length of RQ.
RQ = NQ - NR
RQ = y2 - y1
Step 4 :
Triangle PQR is right angled at R. (PR ⊥ NQ)
By Pythagorean Theorem,
PQ2 = PR2 + RQ2
d2 = (x2 - x1)2 + (y2 - y1)2
By taking positive square root,
d = √[(x2 - x1)2 + (y2 - y1)2]
Given two points (x1, y1) and (x2, y2), the distance between these points is given by the formula
√[(x2 - x1)2 + (y2 - y1)2]
Examples
Example 1 :
Find the distance between the two points given below.
(-12, 3) and (2, 5)
Solution:
Formula for the distance between the two points is
√[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (-12, 3) and (x2, y2) = (2, 5).
= √[(2 + 12)2 + (5 - 3)2]
= √[142 + 22]
= √[196 + 4]
= √200
= √(2 ⋅ 10 ⋅ 10)
= 10√2
So, the distance between the given points is 10√2 units.
Example 2 :
Find the distance between the two points given below.
(-2, -3) and (6, -5)
Solution:
Formula for the distance between the two points is
√[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (-2, -3) and (x2, y2) = (6, -5).
= √[(6 + 2)2 + (-5 + 3)2]
= √[82 + (-2)2]
= √[64 + 4]
= √68
= √(2 ⋅ 2 ⋅ 17)
= 2√17
So, the distance between the given points is 2√17 units.
Example 3 :
If the distance between the two points given below is 2√29, then find the value of k, given that k > 0.
(-7, 2) and (0, k)
Solution:
Distance between the above two points = 2√29
√[(x2 - x1)2 + (y2 - y1)2] = 2√29
Substitute (x1, y1) = (-7, 2) and (x2, y2) = (3, k).
√[(3 + 7)2 + (k - 2)2] = 2√29
√[102 + (k - 2)2] = 2√29
√[100 + (k - 2)2] = 2√29
Square both sides.
100 + (k - 2)2 = (2√29)2
100 + k2 - 2(k)(2) + 22 = 22(√29)2
100 + k2 - 4k + 4 = 4(29)
k2 - 4k + 104 = 116
Subtract 116 from each side.
k2 - 4k - 12 = 0
(k - 6)(k + 2) = 0
k - 6 = 0 or k + 2 = 0
k = 6 or k = -2
Because k > 0, we have
k = 6
Example 4 :
Find the distance between the points A and B in the xy-pane shown below.
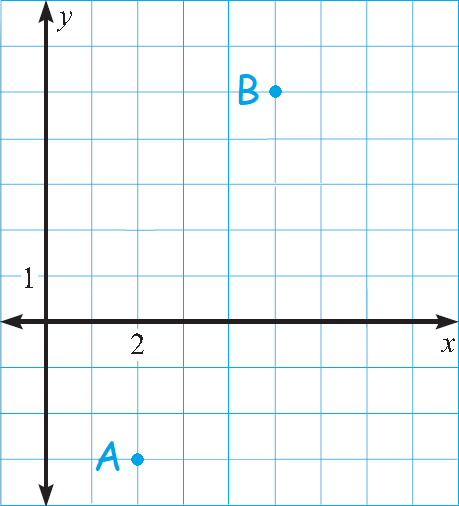
Solution :
Identify the points A and B in the xy-plane above.
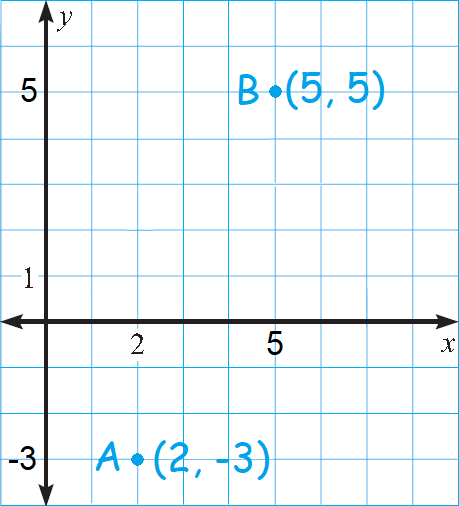
Formula for the distance between the two points is
√[(x2 - x1)2 + (y2 - y1)2]
To find the distance between the points A and B, substitute (x1, y1) = (2, -3) and (x2, y2) = (5, 5).
AB = √[(5 - 2)2 + (5 + 3)2]
AB = √[32 + 82]
AB = √(9 + 64)
AB = √73 units
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Integration Problems Worksheet
Mar 03, 21 07:44 AM
Integration Problems Worksheet
-
Integrating Trigonometric Functions
Mar 03, 21 06:39 AM
Integrating Trigonometric Functions
-
Practice Questions on Integration
Mar 03, 21 06:19 AM
Practice Questions on Integration
