DISTANCE WORD PROBLEMS WORKSHEET WITH SOLUTIONS

Problem 1 :

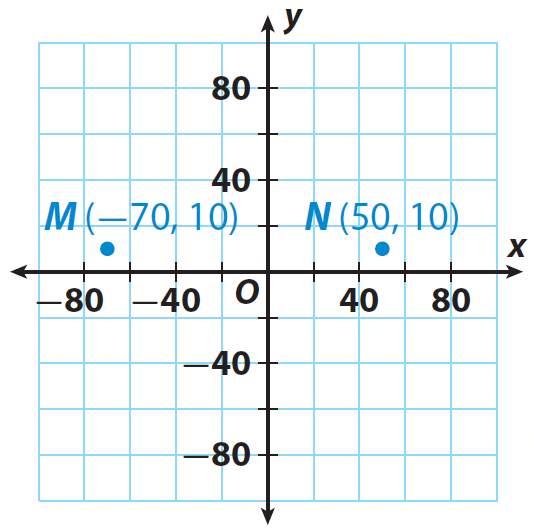
The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouses at M(−70, 10) and N(50, 10). How long does it take a truck that drives 40 miles per hour to travel from warehouse M to warehouse N ?

Problem 2 :

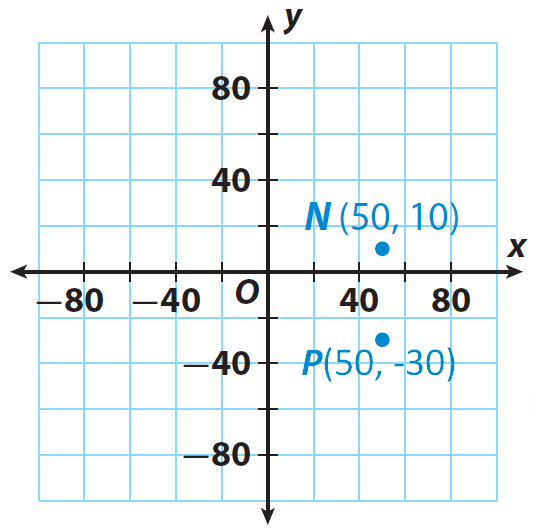
The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouse at and N(50, 10) and a store is located at P(50, -30). How long will it take a truck driving at 50 miles per hour to drive from warehouse N to this store ?

Detailed Answer Key

Problem 1 :

The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouses at M(−70, 10) and N(50, 10). How long does it take a truck that drives 40 miles per hour to travel from warehouse M to warehouse N ?

Solution :

Let us locate the points M(−70, 10) and N(50, 10) on the graph. 

Step 1 :

Identify the important information.

One warehouse is located at M(−70, 10). The other is at N(50, 10).

A truck drives from M to N at a speed of 40 miles per hour.

Step 2 :

Find the distance between M and N by adding the absolute values of the x-coordinates of the points.

Find the time it takes the truck to drive this distance by using this relationship : distance = rate · time.

Step 3 :

Add the absolute values of the x-coordinates to find the distance between point M and point N on the grid.

|-70| + |50| = 70 + 50 = 120

The warehouses are 120 miles apart.

The truck drives 120 miles at 40 mi/h. Because 120 = 40(3), it takes the truck 3 hours to travel from M to N.

Justify and Evaluate :

We found the sum of the absolute values of the x-coordinates to find the horizontal distance on the grid.

Then, we used the formula 

Distance  =  Rate · Time

to find the time it takes to drive that distance.

Problem 2 :

The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouse at and N(50, 10) and a store is located at P(50, -30). How long will it take a truck driving at 50 miles per hour to drive from warehouse N to this store ?

Solution :

Let us locate the points N(50, 10) and P(50, -30) on the graph. 

Step 1 :

Identify the important information.

The warehouse is located at N(50, 10) and the store is located at P(50, -30) and 

A truck drives from  N to P at a speed of 50 miles per hour.

Step 2 :

The line which connects N and P is parallel to y-axis.

Find the distance between N and P by adding the absolute values of the y-coordinates of the points.

Find the time it takes the truck to drive this distance by using this relationship : distance = rate · time.

Step 3 :

Add the absolute values of the y-coordinates to find the distance between point N and point P on the grid.

|10| + |-30| = 10 + 30 = 40

The store P and the warehouse N are 40 miles apart.

The truck drives 40 miles at 50 mi/h. Because 40 = 50(0.8), it takes the truck 0.8 hours or 48 minutes to travel from N to P.

(0.8 hrs  =  0.8x60  =  48 minutes)

Justify and Evaluate :

We found the sum of the absolute values of the y-coordinates to find the vertical distance on the grid.

Then, we used the formula 

Distance  =  Rate · Time

to find the time it takes to drive that distance.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.