DISTRIBUTIVE PROPERTY OF SET

Example 1 :

Given :

A = {0, 1, 2, 3, 4}

B = {1, -2, 3, 4, 5, 6}

C = {2, 4, 6, 7}

Show that

Au(BnC) = (AuB)n(AuC)

Also, verify the above using Venn diagram.

Solution :

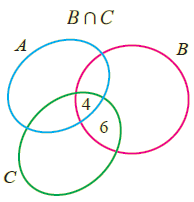
BnC = {1, -2, 3, 4, 5, 6} n {2, 4, 6, 7}.

 BnC = {4, 6}

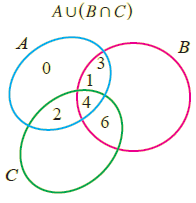
Au(BnC) = {0, 1, 2, 3, 4} u {4, 6}

  Au(BnC) = {0, 1, 2, 3, 4, 6} -----(1)

AuB = {0, 1, 2, 3, 4} u {1, - 2, 3, 4, 5, 6}

= {-2, 0, 1, 2, 3, 4, 5, 6}

AuC = {0, 1, 2, 3, 4} u {2, 4, 6, 7}

= {0, 1, 2, 3, 4, 6, 7}

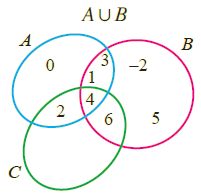
(AuB)n(AuC) = {-2, 0, 1, 2, 3, 4, 5, 6} n {0, 1, 2, 3, 4, 6, 7}

(AuB)n(AuC) = {0, 1, 2, 3, 4, 6} ----(2)

From (1) and (2),

Au(BnC) = (AuB)n(AuC)

Venn Diagram :

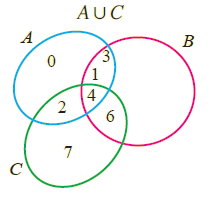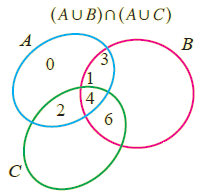Example 2 :

Given :

A = {x : - 3 ≤ x < 4, x ∊ R}

B = {x ; x < 5, x ∊ N}

C = {- 5, - 3, -1, 0, 1, 3}

Show that

An(BuC) = (AnB)u(AnC)

Solution :

A = {x : - 3 ≤ x < 4, x ∊ R} ----> A = {-3, -2, -1, 0, 1, 2, 3}

B = {x ; x < 5, x ∊ N} ----> B = {1, 2, 3, 4}

C = {- 5, - 3, -1, 0, 1, 3}

BuC = {1, 2, 3, 4} u {- 5, - 3, - 1, 0, 1, 3}

  BuC = {-5, -3, -1, 0, 1, 2, 3, 4}

An(BuC) = {-3, -2, -1, 0, 1, 2, 3} n {-5, -3, -1, 0, 1, 2, 3, 4}

An(BuC) = {-3, -1, 0, 1, 2, 3} ----(1)

AnB = {-3, -2, -1, 0, 1, 2, 3} n {1, 2, 3, 4}

AnB = {1, 2, 3}

AnC = {-3, -2, -1, 0, 1, 2, 3} n {- 5, - 3, - 1, 0, 1, 3}

AnC = {-3, -1, 0, 1, 2, 3}

(AnB) u (AnC) = {1, 2, 3} U {-3, -1, 0, 1, 2, 3}

(AnB) u (AnC) = {-3, -1, 0, 1, 2, 3} ----(2)

From (1) and (2),

An(BuC) = (AnB)u(AnC)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.