DIVIDING COMPLEX NUMBERS

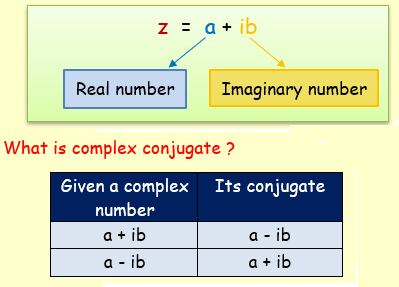
What is complex number ?

A complex number is the sum of a real number and an imaginary number. A complex number is of the form

a + ib

and its represented by ‘z’.

Write the complex number in standard form :

Example 1 :

2/(3 – i)

Solution :

Given, 2/(3 – i)

Multiply the numerator and denominator by the conjugate of the denominator 3 – i. That is 3 + i

= [2/(3 – i)] · (3 + i)/(3 + i)

= 2(3 + i) / (3 – i) (3 + i)

= 2(3 + i) / (3² - i²)

= 2(3 + i) / (9 + 1)

= 2(3 + i) / 10

= (3 + i) / 5

= (3/5) + (1/5)i

So, the standard form is 3/5 + 1/5i

Example 2 :

(5 + i)/(2 – 3i)

Solution :

Given, (5 + i)/(2 – 3i)

Multiply the numerator and denominator by the conjugate of the

Conjugate = 2 + 3i

[(5 + i)/(2 – 3i)] · [(2 + 3i)/(2 + 3i)]

= (5 + i) (2 + 3i) / (2 – 3i) (2 + 3i)

= (10 + 15i + 2i + 3i²) / (2² - (3i)²)

= (10 + 17i - 3) / (4 + 9)

= (7 + 17i) / 13

= (7/13) + (17/13)i

So, the standard form is 7/13 + 17/13i

Example 3 :

1/(2 + i)

Solution :

Given, 1/(2 + i)

Multiply the numerator and denominator by the conjugate of the denominator 2 + i. That is 2 – i

= [1/(2 + i)] [(2 - i) / (2 - i)]

= (2 - i) / (2 + i)(2 - i)

= (2 - i) / (2² - i²)

= (2 - i) / (4 + 1)

= (2 - i) / 5

= (2/5) - (1/5)i

So, the standard form is 2/5 - 1/5i

Example 4 :

i/(2 - i)

Solution :

Given, i/(2 - i)

Multiply the numerator and denominator by the conjugate of the denominator 2 - i. That is 2 + i

= [i/(2 - i)] [(2 + i) / (2 + i)]

= i (2 + i) / (2 - i)(2 + i)

= i (2 + i) / (2² - i²)

= (2i + i²) / (4 + 1)

= (2i - 1) / 5

= (-1 + 2i)/5

= (-1/5) + (2/5)i

So, the standard form is (-1/5) + (2/5)i.

Example 5 :

(2 + i)/(2 – i)

Solution :

Given, (2 + i)/(2 – i)

Multiply the numerator and denominator by the conjugate of the denominator 2 - i. That is 2 + i

= [(2 + i)/(2 – i)] [(2 + i) / (2 + i)]

= (2 + i)(2 + i) / (2 – i)(2 + i)

= (2 + i)² / (2² - i²)

= [4 + i² + 2(2)i] / (4 + 1)

= [4 - 1 + 4i] / 5

= (3 + 4i)/5

= (3/5) + (4/5)i

So, the standard form is 3/5 + 4/5i

Example 6 :

(2 + i)/3i

Solution :

Given, (2 + i)/3i

Multiply the numerator and denominator by the conjugate of the denominator 3i. That is -3i

= [(2 + i)/3i] [-3i/-3i]

= -3i(2 + i) / (-9i²)

= (-6i - 3i²) / 9

= (-6i - 3(-1)) / 9

= (-6i + 3) / 9

= (3/9) - (6i/9)

= (1/3) - (2i/3)

So, the standard form is 1/3 - 2/3i

Example 7 :

(2 + i)²(-i)/(1 + i)

Solution :

Given, (2 + i)²(-i)/(1 + i)

Multiply the numerator and denominator by the conjugate of the denominator 1 + i. That is 1 – i

(2 + i)²(-i)  =  (4 + i² +4i)(-i)

=  (4 - 1  + 4i)(-i)

=  (3 + 4i)(-i)

=  3i - 4i²

=  3i + 4

 (3i + 4)/(1 + i)  =  [(3i + 4)/(1 + i)] [(1 - i)/(1 - i)]

=  (-3+7i+4)/(1+1)

=  (1+7i)/2

=  1/2 + (7/2)i

So, the standard form is 1/2 + (7/2)i.

Example 8 :

(2 - i)(1 + 2i)/(5 + 2i)

Solution :

Given, (2 - i)(1 + 2i)/(5 + 2i)

= (2 - i)(1 + 2i)/(5 + 2i)

= (2 + 4i - i - 2i²)/(5 + 2i)

= (2 + 3i + 2)/(5 + 2i)

= (4 + 3i) / (5 + 2i)  

Multiply the numerator and denominator by the conjugate of the denominator 5 + 2i. That is 5 - 2i

= [(4 + 3i) / (5 + 2i)] [(5 - 2i)/(5 - 2i)]

= (4 + 3i) (5 + 2i) / (5 - 2i)(5 - 2i)

= (4 + 3i) (5 + 2i) / (5 + 2i)(5 - 2i)

= (20 + 8i + 15i + 6i²) / (5² - (2i)²)

= (20 + 23i - 6) / (25 + 4)

= (14 + 23i) / 29

= (14/29) + (23/29)i

So, the standard form is (14/29) + (23/29)i.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.