DIVIDING RATIONAL EXPRESSIONS WORKSHEET

Simplify each expression. 

1.  [(x² - 2x)/(2x + 4)] ÷ [(5x - 10)/(3x + 6)]

2.  [(6x + 6)/(x² - 4)] ÷ [(3x + 3)/(x² + 6x + 8)]

3.  [(a + b)/(a - b)] ÷ [(a³ + b³)/(a³ - b³)]

4.  (5ab/15cd) ÷ (32ad/4bc)

5.  [(x² - 2x + 1)/(x² - 3x + 2)] ÷ [(6x - 6)/(3x - 6)]

6.  [(x² - 25)/(x + 3)] ÷  [(x + 5)²/(x² - 9)]

7.  [(x² - 9y²)/(3x - 3y)] ÷ [(x + 3y)/(x - y)]

8.  [(x² - 16)/(x - 2)] ÷ [(x³ + 64)/(x - 2)]

9.  [(p² - 1)/p] ÷ [(p³ - 1)/p³]

10.  [(px - 2p)/(qx - 3q)] ÷ [(ax - 2a)/(bx - 3b)]

11.  [8(10 - x) / (x + 1)(x - 10)] ÷ [(x - 8) / (x - 8)(x + 1)]

12.  [(6x³ + 18x²) / 6x²] ÷ [(x + 3)/6x²]

1. Answer :

=  [(x² - 2x)/(2x + 4)] ÷ [(5x - 10)/(3x + 6)]

Invert the second rational expression and multiply.

=  [(x² - 2x)/(2x + 4)] ⋅ [(3x + 6)/(5x - 10)]

Multiply numerators and denominators. 

=  [(x² - 2x)(3x + 6)] /[(2x + 4)(5x - 10)]

Factor the numerator and denominator. 

=  [x(x - 2)3(x + 2)] /[2(x + 2)5(x - 2)]

=  [3x(x - 2)(x + 2)] /[10(x + 2)(x - 2)]

Cancel common factors.  

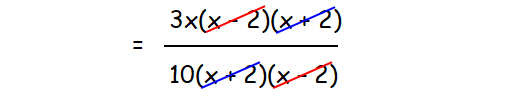
=  3x/10

2. Answer :

=  [(6x + 6)/(x² - 4)] ÷ [(3x + 3)/(x² + 6x + 8)]

Invert the second rational expression and multiply.

=  [(6x + 6)/(x² - 4)] ⋅ [(x² + 6x + 8)/(3x + 3)]

Multiply numerators and denominators. 

=  [(6x + 6)(x² + 6x + 8)] / [(x² - 4)(3x + 3)]

Factor the numerator and denominator. 

=  [6(x + 1)(x + 2)(x + 4)] / [(x + 4)(x - 4)3(x + 1)]

=  [6(x + 1)(x + 2)(x + 4)] / [3(x + 4)(x - 4)(x + 1)]

Cancel common factors. 

=  [6(x + 2)] / [3(x - 4)]

=  2(x + 2)/(x - 4)

3. Answer :

=  [(a + b)/(a - b)] ÷ [(a³ + b³)/(a³ - b³)]

Invert the second rational expression and multiply.

=  [(a + b)/(a - b)] ⋅ [(a³ - b³)/(a³ + b³)]

Multiply numerators and denominators. 

=  [(a + b)(a³ - b³)]/[(a - b)(a³ + b³)]

Factor the numerator and denominator. 

=  [(a + b)(a - b)(a² + ab + b²)]/[(a - b)(a + b)(a² - ab + b²)]

Cancel common factors. 

=  (a² + ab + b²) / (a² - ab + b²)

4. Answer :

=  (5ab/15cd) ÷ (32ad/4bc)

Invert the second rational expression and multiply.

=  (5ab/15cd) ⋅ (4bc/32ad)

Multiply numerators and denominators. 

=  (5ab ⋅ 4bc) / (15cd ⋅ 32ad)

=  20ab²c / 480acd²

Cancel common factors. 

=  b²/24d²

5. Answer :

=  [(x² - 2x + 1)/(x² - 3x + 2)] ÷ [(6x - 6)/(3x - 6)]

Invert the second rational expression and multiply.

=  [(x² - 2x + 1)/(x² - 3x + 2)] ⋅ [(3x - 6)/(6x - 6)]

Multiply numerators and denominators. 

[(x² - 2x + 1)(3x - 6)] / [(x² - 3x + 2)(6x - 6)]

Factor the numerator and denominator. 

=  [(x - 1)(x - 1)3(x - 2)] / [(x - 2)(x - 1)6(x - 1)]

=  [3(x - 1)(x - 1)(x - 2)] / [6(x - 2)(x - 1)(x - 1)]

Cancel common factors. 

=  3/6

=  1/2

6. Answer :

=  [(x² - 25)/(x + 3)] ÷ [(x + 5)²/(x² - 9)]

Invert the second rational expression and multiply.

=  [(x² - 25)/(x + 3)] ⋅ [(x² - 9)/(x + 5)²]

Multiply numerators and denominators. 

=  [(x² - 25)(x² - 9)] ⋅ [(x + 3)(x + 5)²]

Factor the numerator and denominator. 

=  [(x + 5)(x - 5)(x + 3)(x - 3)] / [(x + 3)(x + 5)(x + 5)]

Cancel common factors. 

=  [(x - 5)(x - 3)] / (x + 5)

7. Answer :

=  [(x² - 9y²)/(3x - 3y)] ÷ [(x + 3y)/(x - y)]

Invert the second rational expression and multiply.

=  [(x² - 9y²)/(3x - 3y)] ⋅ [(x - y)/(x + 3y)]

Multiply numerators and denominators. 

=  [(x² - 9y²)(x - y)] / [(3x - 3y)(x + 3y)]

Factor the numerator and denominator. 

=  [(x + 3y)(x - 3y)(x - y)] / [3(x - y)(x + 3y)]

Cancel common factors. 

=  (x - 3y)/3

8. Answer :

=  [(x² - 16)/(x - 2)] ÷ [(x³ + 64)/(x - 2)]

Invert the second rational expression and multiply.

=  [(x² - 16)/(x - 2)] ⋅ [(x - 2)/(x³ + 64)]

Multiply numerators and denominators. 

=  [(x² - 16)(x - 2)] / [(x - 2)(x³ + 64)]

=  [(x² - 4²)(x - 2)] / [(x - 2)(x³ + 4³)]

Factor the numerator and denominator. 

=  [(x + 4)(x - 4)(x - 2)] / [(x - 2)(x + 4)(x² - 4x + 16)]

Cancel common factors. 

=  (x - 4)/(x² - 4x + 16)

9. Answer :

=  [(p² - 1)/p] ÷ [(p³ - 1)/p³]

Invert the second rational expression and multiply.

=  [(p² - 1)/p] ⋅ [p³/(p³ - 1)]

Multiply numerators and denominators. 

=  [(p² - 1)/p] ⋅ [p³/(p³ - 1)]

=  [p³(p² - 1)] / [p(p³ - 1)]

=  p³(p² - 1²) / p(p³ - 1³)

Factor the numerator and denominator. 

=  [p³(p + 1)(p - 1)] / [p(p - 1)(p² + p + 1)]

Cancel common factors. 

=  [p²(p + 1)] / (p² + p + 1)

10. Answer :

=  [(px - 2p)/(qx - 3q)] ÷ [(ax - 2a)/(bx - 3b)]

Invert the second rational expression and multiply.

=  [(px - 2p)/(qx - 3q)] ⋅ [(bx - 3b)/(ax - 2a)]

Multiply numerators and denominators. 

=  [(px - 2p)(bx - 3b)] / [(qx - 3q)(ax - 2a)]

Factor the numerator and denominator. 

=  [p(x - 2)b(x - 3)] / [q(x - 3)a(x - 2)]

=  [bp(x - 2)(x - 3)] / [aq(x - 3)(x - 2)]

Cancel common factors. 

=  bp/aq

11. Answer :

= [8(10 - x) / (x + 1)(x - 10)] ÷ [(x - 8) / (x - 8)(x + 1)]

= [8(10 - x) / (x + 1)(x - 10)] ⋅ [(x - 8)(x + 1)/(x - 8)]

Factoring negative from 10 - x, we get

= [-8(x - 10) / (x + 1)(x - 10)] ⋅ [(x - 8)(x + 1)/(x - 8)]

= [-8/(x + 1)] ⋅ (x + 1)

= -8

12. Answer :

= [(6x³ + 18x²) / 6x²] ÷ [(x + 3)/6x²]

= [(6x³ + 18x²)/ 6x²] ⋅ [6x²/(x + 3)]

= (6x³ + 18x²) / (x + 3)

= 6x²(x + 3) / (x  +3)

= 6x²

6x² is the answer

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.