DIVISION ALGORITHM PROBLEMS AND SOLUTIONS

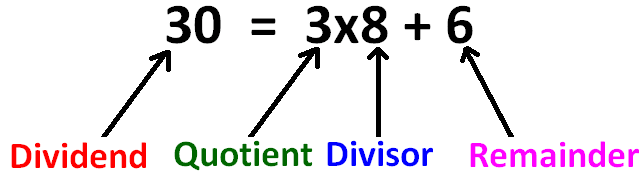
When we divide a number by another number, the division  algorithm is, the sum of product of quotient & divisor and remainder is equal to dividend.

More clearly, 

Dividend  = Quotient x Divisor + Remainder

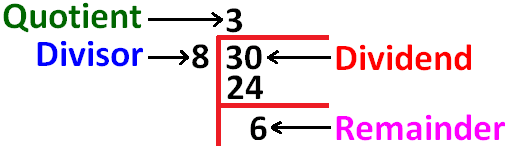
When we divide a number by another number, we will have the terms dividend, divisor, quotient and remainder.

• The number which we divide is called the dividend.
• The number by which we divide is called the divisor.
• The result obtained is called the quotient.
• The number left over is called the remainder.

More clearly, Division Algorithm :

Division Algorithm

Solving Problems using Division Algorithm

Problem 1 :

What is dividend, when divisor is 17, the quotient is 9 and the remainder is 5 ?

(A)  153  (B)  156  (C)  158  (D)  None of these

Solution :

Using division algorithm

Dividend  =  Divisor x quotient + Remainder

Dividend  =  17 x 9 + 5

Dividend  =  153 + 5

Dividend  =  158

Hence the required dividend is 158.

Problem 2 :

When the integer n is divided by 8, the remainder is 3. What is the remainder if 6n is divided by 8?

A) 0     B) 1     C) 2     D) 3     E) 4

Solution :

Using division algorithm

Dividend  =  Divisor x quotient + Remainder

From the given information, we have

n  =  8q + 3

To find the remainder, when 6n is divided by 8, we multiply 6 on both sides.

6n  =  48q + 18

6n  =  48q + 16 + 2

Factoring out 8 from 48 and 16, we get

6n  =  8(6q + 2) + 2

8(6q + 2) is the multiple of 8 and remainder is 2.

Hence we get 2 as remainder, while dividing 6n by 8.

Problem 3 :

On dividing 12401 by a certain number, we get 76 as quotient and 13 as remainder. What is the divisor ?

Solution :

Let x be the divisor.

Dividend  =  12401, divisor  =  x, quotient  =  76 and remainder  =  13.

12401  =  76x + 13

12401 - 13  =  76x

Solving for x, we get the divisor.

76x  =  12388

x  =  12388/76

x  =  163

Hence the divisor is 163.

Problem 4 :

On dividing a certain number by 342, we get 47 as remainder. If the same number is divided by 18, what will be the remainder ?

Solution :

Let x be the quotient on dividing a number by 342, which yields the remainder 47.

By applying the above information in division algorithm, we get

Number  =  342x + 47

Now, we should divide the same number by 18 and find the remainder.

Representing 342x + 47 as the multiple of 18, we get

342x + 47  =  (18 ⋅ 19x) + 36 + 11

342x + 47  =  (18 ⋅ 19x) + 2 ⋅ 18 + 11

Factoring out 18, we get

342x + 47  =  18(19x + 2) + 11

18(19x + 2) is the multiple of 18.

Hence the remainder is 11.

Problem 5 :

If a positive integer n is divided by 5, the remainder is 3. Which of the numbers below yields a remainder of 0 when it is divided by 5 ?

A) n + 3     B) n + 2     C) n - 1     D) n - 2     E) n + 1

Solution :

It can be solved easily by doing a small assumption.

If n = 8

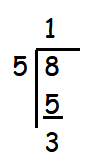It is possible for all values of n which is divisible by 5 and more than 3. If we add 2 by n, we will get the remainder as 0.

Hence the answer is n + 2.

Note :

Using the concept division algorithm, we may solve this problem.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.