DOMAIN AND RANGE OF A RELATION

In the scoring system of some track meets, first place is worth 5 points, second place is worth 3 points, third place is worth 2 points, and fourth place is worth 1 point.

This scoring system is a relation, so it can be shown as ordered pairs, {(1, 5),  (2, 3), (3, 2), (4, 1)}. 

The domain of a relation is the set of first coordinates (or x-values) of the ordered pairs. The range of a relation is the set of second coordinates (or y-values) of the ordered pairs.

The domain of the track meet scoring system is {1, 2, 3, 4}. The range is {5, 3, 2, 1}.

Solved Problems

Problem 1 : 

Find the domain and range of the relation shown in the graph below. 

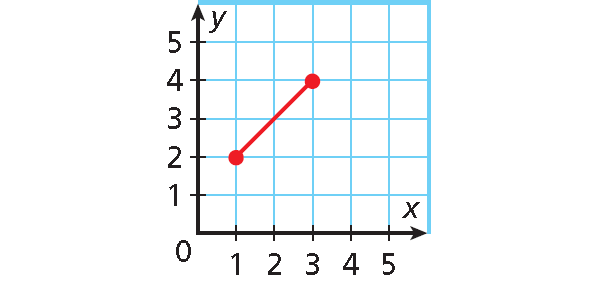
Solution : 

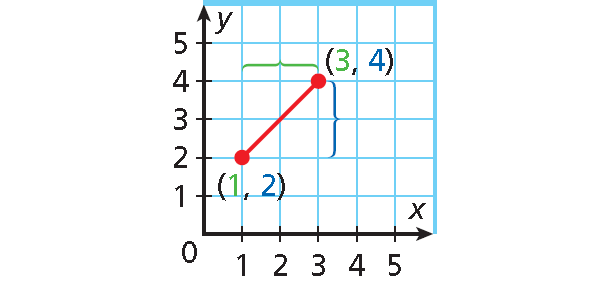
The domain is all x-values from 1 through 3, inclusive.

Domain : 1 ≤ x ≤ 3

The range is all y-values from 2 through 4, inclusive.

Range : 2 ≤ y ≤ 4

Problem 2 :

Find the domain and range of the relation shown in the mapping diagram below. 

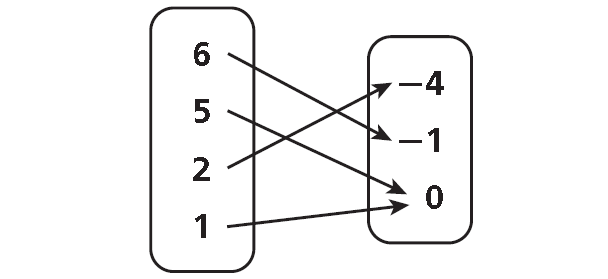
Solution : 

Domain  =  {1, 2, 5, 6}

Range  =  {-4, -1, 0}

Problem 3 :

Find the domain and range of the relation shown in the mapping diagram below. 

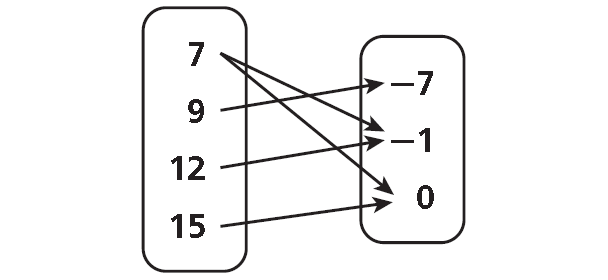
Solution : 

Domain  =  {7, 9, 12, 15}

Range  =  {-7, -1, 0}

Problem 4 :

Find the domain and range of the relation shown in the table below. 

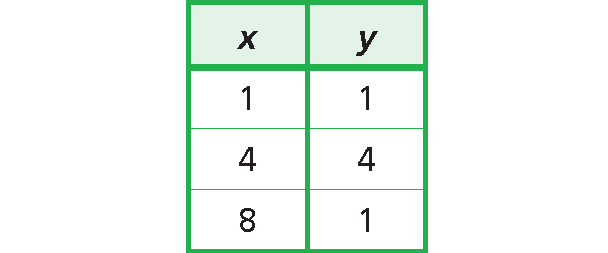
Solution : 

Domain  =  {1, 4, 8}

Range  =  {1, 4}

Problem 5 :

Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. If R is the relation which maps the elements from A to B using the rule f(x) = x², then find the domain and range of R. 

Solution :

R maps the elements from A to B using the rule

f(x)  =  x²

Then, we have

f(1)  =  1²  =  1

f(2)  =  2²  =  4

f(3)  =  3²  =  9

f(4)  =  4²  =  16

So, 

R  =  {(1, 1), (2, 4), (3, 9), (4, 16)}

Therefore, 

Domain (R)  =  {1, 2, 3, 4}

Range (R)  =  {1, 4, 9, 16}

Problem 6 : 

Let A  =  {1, 2, 3} and B  =  {5, 6, 7, 8}. 

R is the relation which maps the elements from A to B as shown below. 

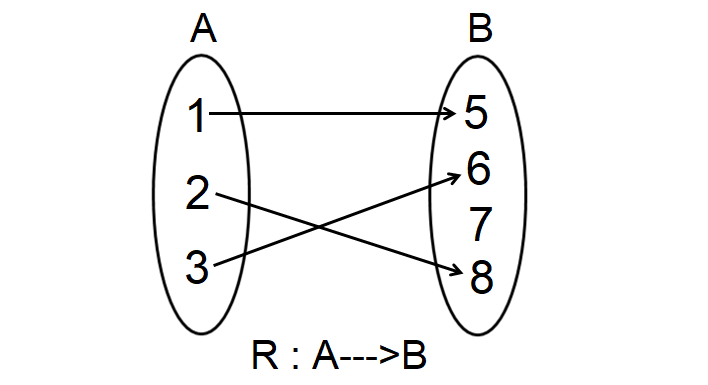
Find the domain and range of R.

Solution : 

From the arrow diagram shown above, 

R  =  {(1, 5), (2, 8), (3, 6)}

Therefore, 

Domain (R)  =  {1, 2, 3}

Range (R)  =  {5, 6, 8}

Problem 7 : 

Let X  =  {a, b, c} and Y  =  {d, e, f, g}. 

R is the relation which maps the elements from X to Y as shown below. 

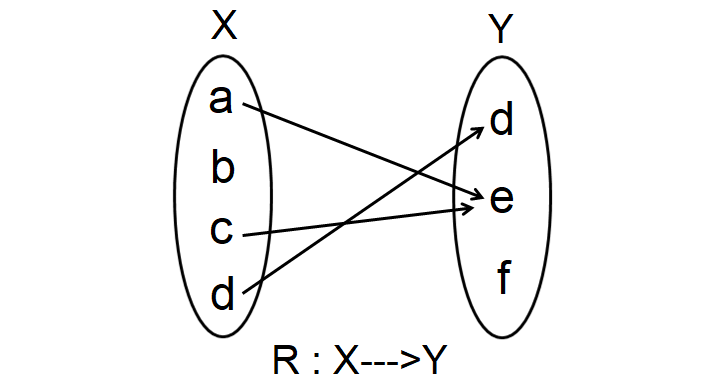
Find the domain and range of R.

Solution : 

From the arrow diagram shown above, 

R  =  {(a, e), (c, e), (d, f)}

Therefore, 

Domain (R)  =  {a, c, d}

Range (R)  =  {d, e}

Problem 8 : 

Let R be a relation defined as given below.  

R  =  {(1, 1), (2, 3), (3, 4), (2, 7)}

Find the domain and range of R and R^-1. Discuss the relationship between the domain and range of R and R^-1. 

Solution : 

R  =  {(1, 1), (2, 3), (3, 4), (2, 7)}

Domain and range of R : 

Domain (R)  =  {1, 2, 3}

Range (R)  =  {1, 3, 4, 7}

Find inverse relation R^-1 :

R^-1  =  {(1, 1), (3, 2), (4, 3), (7, 2)}

Domain and range of R^-1 : 

Domain (R^-1)  =  {1, 3, 4, 7}

Range (R^-1)  =  {1, 2, 3}

Clearly,

Domain (R^-1)  =  Range (R)

Range (R^-1)  =  Domain (R)

Problem 9 :

Graph the function for the given domain.

f(x) = x² - 3; D = {-2, -1, 0, 1, 2}

Solution :

f(x) = x² - 3

D = {-2, -1, 0, 1, 2}

When x = 2

f(2) = 2² - 3

= 4 - 3

f(2) = 1

Writing down the values of x and y as ordered pairs, we get

(-2, 1) (-1, -2) (0, -3) (1, -2) (2, 1)

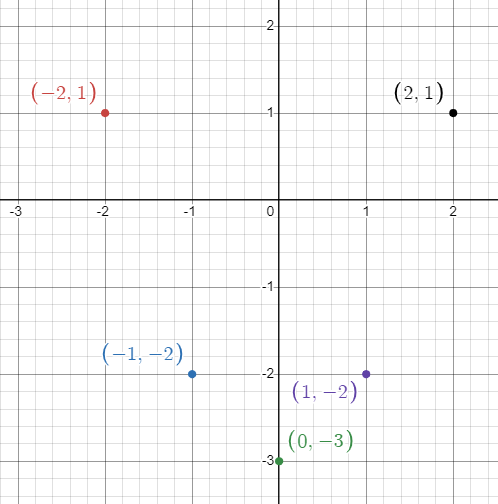
Problem 10 :

Graph the function for the given domain.

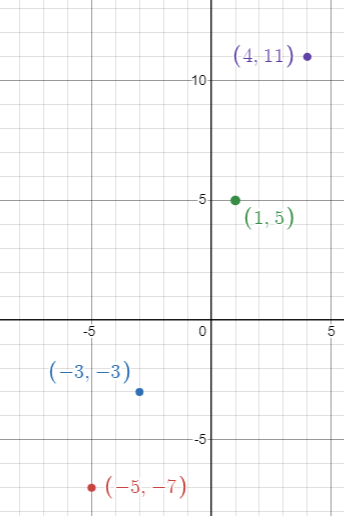
-2x + y = 3; D = {-5, -3, 1, 4}

Solution :

-2x + y = 3

D = {-5, -3, 1, 4}

Writing down the values of x and y as ordered pairs, we get

(-5, -7) (-3, -3) (1, 5) (4, 11)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.