DOMAIN CODOMAIN AND RANGE OF A FUNCTION

Let f be a function and we have 

f : A ---> B

Then, A is called the domain, B is called the co-domain of f. 

The set f(A)  =  {f(x) : x ∈ A} is called the range.

Example : 

Let A  =  {1, 2, 3, 4} and B  =  {1, 4, 9, 16, 25}

Let us consider the rule f(x)  =  x² to map elements from A to B. 

Then, we have 

f(1)  =  1²  =  1

f(2)  =  2²  =  4

f(3)  =  3²  =  9

f(4)  =  4²  =  16

Clearly each element in A has a unique image in B. 

So, f : A ---> B : f(x)  =  x² is a function from A to B. 

Here, we have 

Domain (f)  =  A  =  {1, 2, 3, 4}

Co-Domain (f)  =  B  =  {1, 4, 9, 16, 25}

Range (f)  =  {1, 4, 9, 16}

Note : 

If co-domain and range are equal, then the function will be an onto or surjective function. 

If range is a proper subset of co-domain, then the function will be an into function.  

Practice Problems

Problem 1 : 

Let A  =  {1, 2, 3} and B  =  {5, 6, 7, 8}. 

f is the function which maps the elements from A to B as shown below. 

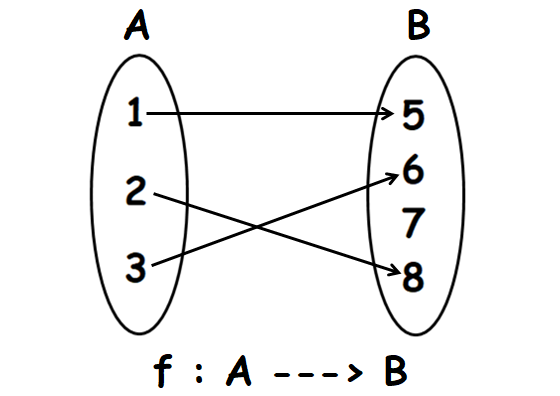
Find, the domain, co-domain and range of f. 

Solution : 

Domain (f)  =  A  =  {1, 2, 3}

Co-domain (f)  =  B  =  {5, 6, 7, 8}

Range (f)  =  {5, 6, 7} 

Problem 2 : 

Let X  =  {a, b, c, d} and Y  =  {d, e, f}. 

f is the function which maps the elements from X to Y as shown below. 

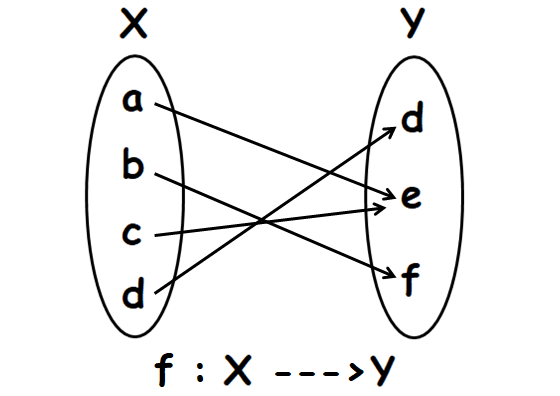
Find, the domain, co-domain and range of f. 

Solution : 

Domain (f)  =  A  =  {a, b, c, d}

Co-domain (f)  =  B  =  {d, e, f}

Range (f)  =  {d, e, f} 

Problem 3 : 

Let A  =  {1, 2, 3} and B  =  {5, 6, 7, 8}. 

f is the function which maps the elements from A to B as shown below. 

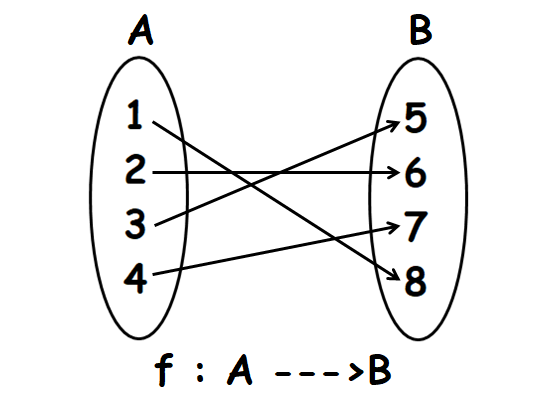
Find, the domain, co-domain and range of f. 

Solution : 

Domain (f)  =  A  =  {1, 2, 3, 4}

Co-domain (f)  =  B  =  {5, 6, 7, 8}

Range (f)  =  {5, 6, 7, 8}

Problem 4 : 

Let X  =  {a, b, c} and Y  =  {d, e, f, g}. 

f is the function which maps the elements from X to Y as shown below. 

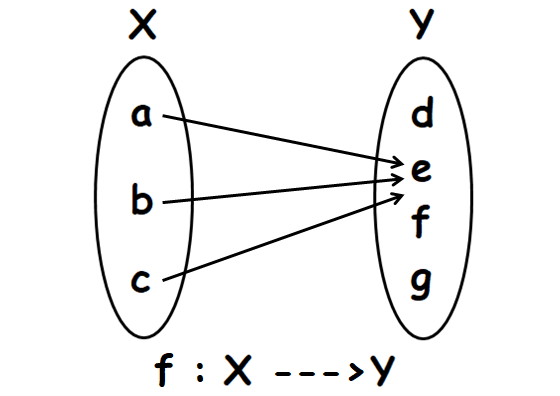
Find, the domain, co-domain and range of f. 

Solution : 

Domain (f)  =  A  =  {a, b, c}

Co-domain (f)  =  B  =  {d, e, f, g}

Range (f)  =  {e} 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.