DRAWING DILATIONS WORKSHEET

Problem 1 :

Construct a dilation of a triangle using a point as the center and  a scale factor of 2.

Problem 2 :

Construct a dilation of a triangle using a point as the center and a scale factor of 1/2.

Problem 3 :

Construct a dilation of a triangle using a point as the center and a scale factor of 2.5.

Problem 4 :

Draw a dilation of rectangle ABCD with

A(2, 2), B(6, 2), C(6, 4) and D(2, 4)

Use the origin as the center and use a scale factor of 1/2. How does the perimeter of the preimage compare to the perimeter of the image?

1. Answer :

Step 1 :

Draw ΔXYZ and choose the center of the dilation C. Use a straightedge to draw lines from C through the vertices of the triangle.

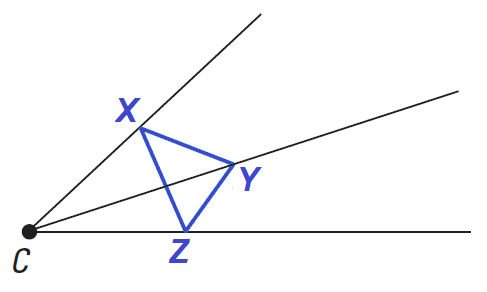
Step 2 :

Use the compass to locate X' on CX so that

CX'  =  2(CX)

Locate Y' and Z' in the same way.

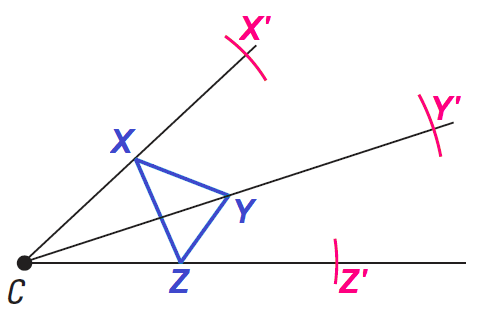
Step 3 :

Connect the points X', Y' and Z'.

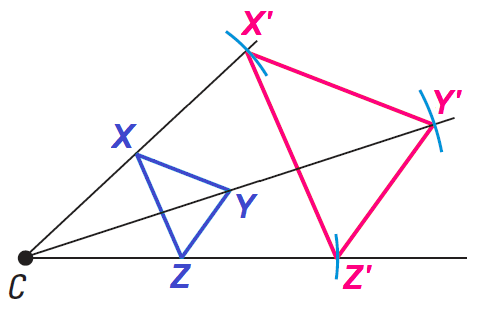
In the construction above, notice that

ΔXYZ ∼ ΔX'Y'Z'

We can prove this by using the SAS and SSS Similarity Theorems.

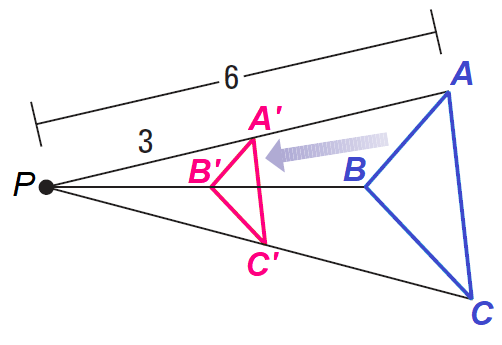
2. Answer :

When we follow the steps explained in problem 1, we will be getting ΔA'B'C' after a dilation of ΔABC using a scale factor 1/2.

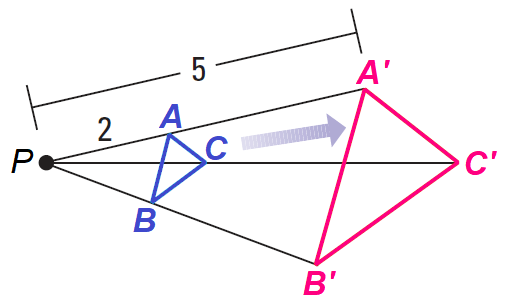
3. Answer :

When we follow the steps explained in problem 1, we will be getting ΔA'B'C' after a dilation of ΔABC using a scale factor 2.5.

4. Answer :

A(2, 2), B(6, 2), C(6, 4) and D(2, 4)

Because the center of the dilation is the origin, we can find the image of each vertex by multiplying its coordinates by the scale factor 1/2.

P(2, 2) ----> P'(1, 1)

Q(6, 2) ----> Q'(3, 1)

R(6, 4) ----> R'(3, 2)

S(2, 4) ----> S'(1, 2)

Let us plot the above points in xy-plane.

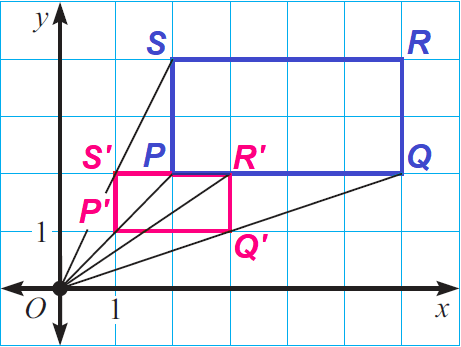
From the graph, we can see that the preimage has a perimeter of 12 and the image has a perimeter of 6. A preimage and its image after a dilation are similar figures. Therefore, the ratio of the perimeters of a preimage and its image is equal to the scale factor of the dilation.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.