EASY WAY TO FIND SQUARE ROOT OF THREE-DIGIT AND FOOUR-DIGIT NUMBERS
What is square root?
Square root is the inverse operation of squaring a number. Remember that the square is of a number is the number times itself. For example, if you want to find square root of a number 16, find the number when it is multiplied by itself results 16. They are -4 and 4. So, the square root of 16 is ±4.
√16 = ±4
Important factors that we should memorize before going to know the easy way to find square root of two digit and three digit numbers.
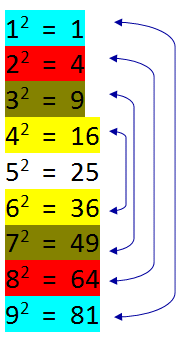
Squares of 1 and 9 have 1 at ones place.
Squares of 2 and 8 have 4 at ones place.
Squares of 3 and 7 have 9 at ones place.
Squares of 4 and 6 have 6 at ones place..
Square of 5 has have 5 at ones place.
|
Numbers |
Squares |
Ones Place |
|
1 2 3 4 5 6 7 8 9 |
1 4 9 16 25 36 49 64 81 |
1 4 9 6 5 6 9 4 1 |
Video Lesson
Easy Way to Find Square Root of a Three-Digit Number
Let us try to find square root of 576.
To find the square root 576, first we have to split it up into groups.
The digits which are at ones place and tens place as one group and the digit which is at hundreds place as another group.
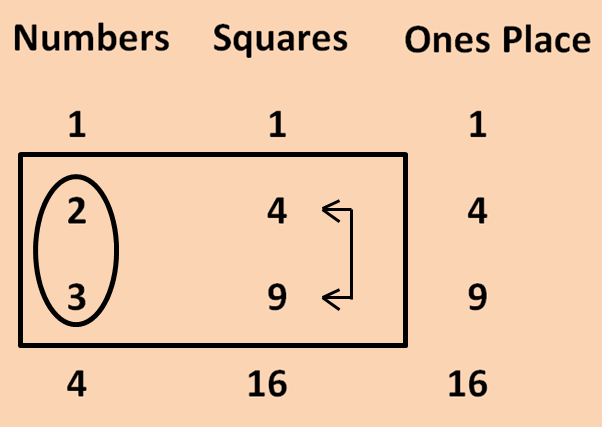
Now, we have to consider the first digit of the given number 576, that is 5. In the squares column above, 5 lies between 4 (the square of 2) and 9 (the square of 3).

Since 4 is smaller than 5, we have to choose 2 from the numbers column which is corresponding to 4 in squares column.
So far, we have found the first digit of square root of 576, that is 2. To choose the second digit, we have to multiply the first digit 2 by its succeeding number 3.
2 x 3 = 6, where 6 is greater than 5 which is in 576. So, we have to choose the smaller number out of 4 and 6 (whose squares are ending with 6, which is at ones place 576).
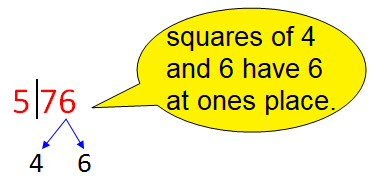
Smaller number is 4. So the second digit is 4.
Square root if 576 is 24.
Easy Way to Find Square Root of a Four-Digit Number
Let us try to find square root of 6241.
First we have to split it up into groups.
The digits which are at ones place and tens place as one group and the digits which are at hundreds place and thousands place as another group.
62|41
Now we have to consider the group which contains 62. In the squares column 62 lies between 49 (the square of 7) and 64 (the square of 8).
Since 49 is smaller than 62, we have to choose 7 (from the numbers column) which is corresponding to 49 in squares column.
So far, we have found the first digit of square root of 6241, that is 7. To choose the second digit, we have to multiply the first digit 7 by its succeeding number 8.
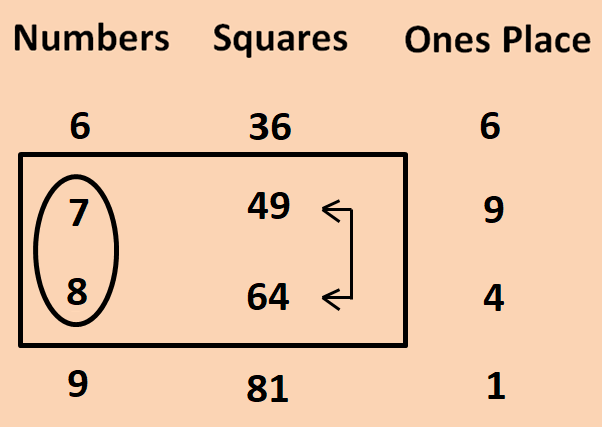
7 x 8 = 56, where 56 is smaller than 62 in 6241. So, we have to choose the larger number out of 1 and 9 (whose squares are ending with 1, which is at ones place 6241).
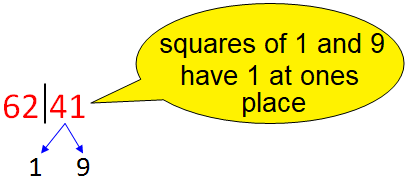
Larger number is 9, so the second digit is 9.
Square root if 6241 is 79.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

