ELIMINATION METHOD
The flow chart shown below explains the steps to be done in solving system of linear equations with two unknowns x and y using elimination method.
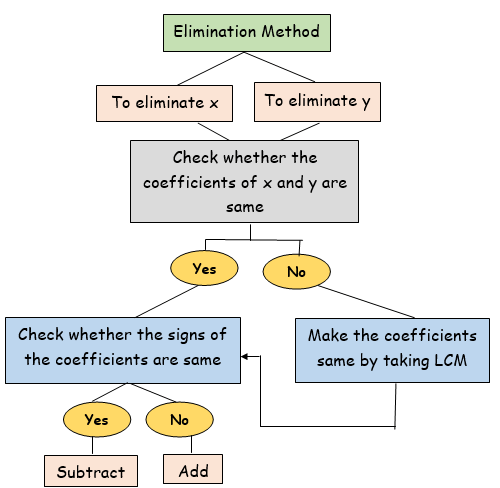
*LCM = Least Common Multiple.
Solving Systems of Linear Equations
Solve each of the following systems by eleimination.
Example 1 :
5x + 2y = 9
3x - 2y = -1
Solution :
5x + 2y = 9 ----(1)
3x - 2y = -1 ----(2)
In the given system of linear equations, we have the same coefficient for y with different signs. So, we have to add the two equations to eliminate y.
(1) + (2) :
Divide both sides by 8.
x = 1
Substitute x = 1 into (1).
5(1) + 2y = 9
5 + 2y = 9
Subtract 5 from both sides.
2y = 4
Divide both sides by 2.
y = 2
Therefore, the solution is
(x, y) = (1, 2)
Example 2 :
3x + 4y = -1
5x + 4y = 1
Solution :
3x + 4y = -1 ----(1)
5x + 4y = 1 ----(2)
In the given system of linear equations, we have the same coefficient for y with the same sign signs. So, we have to subtract the two equations to eliminate y.
(1) - (2) :
Divide both sides by -2.
x = 1
Substitute x = 1 into (1).
3(1) + 4y = -1
3 + 4y = -1
Subtract 3 from both sides.
4y = -4
Divide both sides by 4.
y = -1
Therefore, the solution is
(x, y) = (1, -1)
Example 3 :
2x + y = 7
3x - 2y = 0
Solution :
2x + y = 7 ----(1)
3x - 2y = 0 ----(2)
In the given system of linear equations, we don't have the same coefficient for both x and y. Multiplying (1) by 2, we can get the same coefficient for x, that is 2. Since we have different signs for y, we have to add the equations to eliminate y.
2(1) + (2) :
Divide both sides by 7.
x = 2
Substitute x = 2 into (1).
2(2) + y = 7
4 + y = 7
Subtract 4 from both sides.
y = 3
Therefore, the solution is
(x, y) = (2, 3)
Example 4 :
-3x + 4y = -7
2x - 3y = 6
Solution :
-3x + 4y = -7 ----(1)
2x - 3y = 6 ----(2)
In this system, we can make the coefficients of either x or y same using the least common multiple of the existing coefficients.
The coeffcients of x are 3 and 2 and the least common multiple of them is 6.
Multiplying (1) by 2 and (2) by 3, we can get the same coeffcient for x, that is 6.
Since we have different signs for x, we have to add the equations to eliminate x.
2(1) + 3(2) :
Multiply both sides by -1.
y = -4
Substitute y = -4 into (1).
2x - 3(-4) = 6
2x + 12 = 6
Subtract 12 from both sides.
2x = -6
Divide both sides by 2.
x = -3
Therefore, the solution is
(x, y) = (-3, -4)
Example 5 :
6x - 5y = 9
8x - 17y = -19
Solution :
6x - 5y = 9 ----(1)
8x - 17y = -19 ----(2)
The coeffcients of x are 6 and 8 and the least common multiple of them is 24.
Multiplying (1) by 4 and (2) by 3, we can get the same coeffcient for x, that is 24.
Since we have the same sign for x, we have to subtract the equations to eliminate x.
4(1) - 3(2) :
Multiply both sides by 31.
y = 3
Substitute y = 3 into (1).
6x - 5(3) = 9
6x - 15 = 9
Add 15 to both sides.
6x = 24
Divide both sides by 6.
x = 4
Therefore, the solution is
(x, y) = (4, 3)
Solving Word Problems
Example 6 :
For magic show, $8 is charged for adults and $5 for kids. If a total of 83 tickets were sold for a collection of $520, find the the number of adults tickets and kids tickets sold.
Solution :
Let x and y be the number of adults tickets kids tickets sold respectively.
From the given information,
x + y = 83 ----(1)
8x + 5y = 520 ----(2)
Multiplying (1) by 5, we can get the same coefficient for y, that is 5.
Since we have the same sign for y, we have to subtract the equations to eleiminate y.
5(2) - (1) :
Divide both sides by -3.
x = 35
Substitute x = 35 into (1).
35 + y = 83
Subtract 35 from both sides.
y = 48
Therefore, 35 adult tickets and 48 kids tickets were sold.
Example 7 :
Of two numbers, the difference between three times the first and two times the second is equal to 20. And the sum of three times the first and two times second is equal to 40. Find the two numbers.
Solution :
Let x and y be the two numbers.
From the given information,
3x - 2y = 20 ----(1)
3x + 2y = 40 ----(2)
We have the same coefficient for y with different signs. So, we have to add the two equations to eliminate y.
(1) + (2) :
Divide both sides by 6.
x = 10
Substitute x = 10 into (2).
3(10) + 2y = 40
30 + 2y = 40
Subtract 30 from both sides.
2y = 10
Divide both sides by 2.
y = 5
Therefore, the two numbers are 10 and 5.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

