EQUATION OF A CIRCLE IN STANDARD FORM

We can write the equation of a circle on a coordinate plane, if we know its radius and the coordinates of its center.  Suppose the radius of a circle is r and the center is (h, k). 

Let (x, y) be any point on the circle. The distance between (x, y) and (h, k) is r.

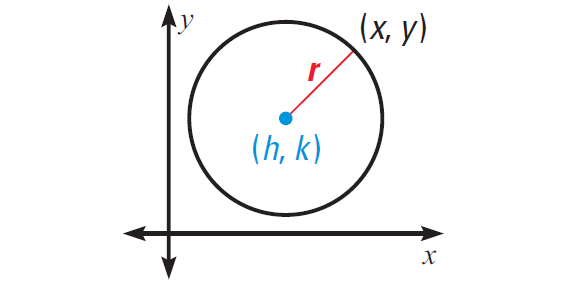
So, we can use the Distance Formula to find the value of r.

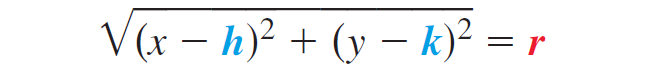
Square both sides to find the equation of the circle in standard form with radius r and center (h, k).

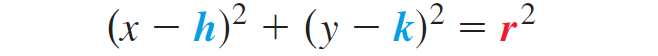
If the center is the origin, then (h, k)  =  (0, 0)

Then the equation of the circle in standard form is

x² + y²  =  r²

Writing Equation of a Circle in Standard Form

Example 1 :

Write the equation of a circle in standard form whose center is (3, 2) and radius is 6.

Solution :

Equation of a circle in standard form :

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (3, 2) and r = 6.

(x - 3)² + (y - 2)²  =  6²

(x - 3)² + (y - 2)²  =  36

Example 2 :

Write the equation of a circle in standard form whose center is (0, -3) and radius is 7.

Solution :

Equation of a circle in standard form :

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (0, -3) and r = 7.

(x - 0)² + [y - (-3)²]  =  7²

x² + (y + 3)²  =  7²

Example 3 :

If two end points of the diameter of a circle are (-1, -2) and (11, 14), find the equation of the circle in standard form. 

Solution :

Using mid point formula, find the mid point of the diameter.  

Mid point of (-1, -2) and (11, 14) : 

=  [(-1 + 11)/2, (-2 + 14)/2]

=  (10/2, 12/2)

=  (5, 6)

Mid point of the diameter is the center of the circle. 

So, the center of the circle is (5, 6). 

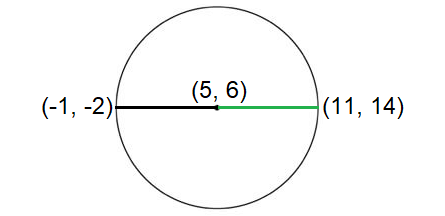
Using distance formula to find the distance between the center and one of the end points of the diameter.

Distance between (5, 6) and (11, 14) :

=  √[(11 - 5)² + (14 - 6)²]

=  √[6² + 8²]

=  √[36 + 64]

=  √100

=  10

Radius of the circle is 10 units. 

Equation of the circle in standard form : 

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (5, 6) and r = 10.

(x - 5)² + (y - 6)²  =  10²

Example 4 :

Write the following general form of equation of the circle in standard form. And find the center and radius. 

x² + y² - 4x + 6y - 12  =  0

Solution :

x² + y² - 4x + 6y - 12  =  0

Write x-terms and y-terms together. 

x² - 4x + y² + 6y - 12  =  0

Completing the square. 

x² - 2(x)(2) + 2² - 2² + y² + 2(y)(3) + 3²- 3² - 12  =  0

(x - 2)² - 2² + (y + 3)² - 3² - 12  =  0

(x - 2)² - 4 + (y + 3)² - 9 - 12  =  0

(x - 2)² + (y + 3)² - 25  =  0

Add 25 to each side. 

(x - 2)² + (y + 3)²  =  25

(x - 2)² + (y + 3)²  =  5²

The above equation of the circle is in standard form.  

Center (h, k)  =  (2, -3)

Radius  =  5

Example 5 :

The point (1 ,2) is on a circle whose center is (5, -1).  Write the equation of the circle in standard equation. 

Solution :

To find the standard equation of the circle, we need to know the center and radius. The center is already given and we need to find the radius.

Using distance formula, we have

Radius  =  √[(5 - 1)² + (-1 - 2)²]

Radius  =  √[4² + (-3)²]

Radius  =  √[16 + 9]

Radius  =  √25

Radius  =  5

Equation of a circle in standard form : 

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (5, -1) and r = 5.

(x - 5)² + [y - (-1)²]  =  5²

Simplify. 

(x - 5)² + (y + 1)²  =  5²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.