EQUATION OF A LINE IN STANDARD FORM WORKSHEET
Problems 1-4 : Write the given equations of lines in standard form :
Problem 1 :
y = -3x + 2
Problem 2 :
y = 2x - 5
Problem 3 :
y = 3x/2 - 1
Problem 4 :
y = 2x/3 - 1/2
Problems 5-6 : Write the equations of the given lines in standard form :
Problem 5 :
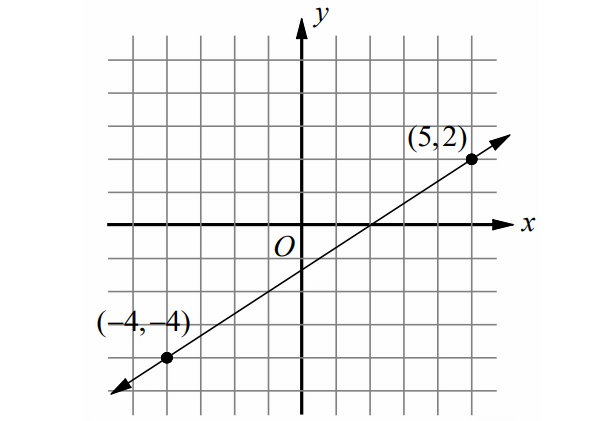
Problem 6 :
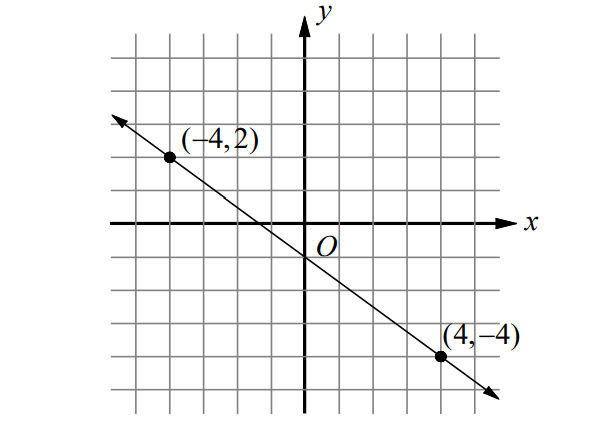
Problem 7 :
Write the equation of a line in standard form that passes through the point (0, -1) and has slope -3.

Answers
1. Answer :
y = -3x + 2
Add 3x to both sides.
3x + y = 2
Subtract 2 from both sides.
3x + y - 2 = 0
2. Answer :
y = 2x - 5
Subtract 2x from both sides.
-2x + y = -5
Multiply both sides by -1.
2x - y = 5
3. Answer :
y = 3x/2 - 1
Multiply both sides of the equation 2.
2(y) = 2(3x/2 - 1)
2y = 2(3x/2) + 2(-1)
2y = 3x - 2
Subtract 3x from both sides.
-3x + 2y = -2
Multiply both sides by -1.
3x - 2y = 2
4. Answer :
y = 2x/3 - 1/2
In the equation above, we find two different denominators 3 and 2.
The least common multiple of (3, 2) = 6.
Multiply both sides of the equation by 6 to get rid of the denominators 3 and 2.
6(y) = 6(2x/3 - 1/2)
6y = 6(2x/3) + 6(-1/2)
6y = 2(2x) + 3(-1)
6y = 4x - 3
Subtract 4x from both sides.
-4x + 6y = -3
Multiply both sides of the equation by -1.
4x - 6y = 3
5. Answer :
Formula to find the slope of a line when two points are given :
Substitute (x1, y1) = (-4, -4) and (x2, y2) = (5, 2).
Equation of the line in slope-intercept form :
y = mx + b
Substitute m = 2/3.
y = 2x/3 + b ----(1)
Substitute one of the two points on the line into the above equation to solve for b.
Substitute (5, 2) into the above equation.
2 = 2(5)/3 + b
2 = 10/3 + b
Subtract 10/3 from both sides.
2 - 10/3 = b
-4/3 = b
Substitute b = -4/3 in (1).
y = 2x/3 - 4/3
Multiply both sides by 3 to get rid of the denominators.
3(y) = 3(2x/3 - 4/3)
3y = 3(2x/3) + 3(-4/3)
3y = 2x - 4
Subtract 2x from both sides.
-2x + 3y = -4
Multiply both sides of the equation by -1.
2x - 3y = 4
6. Answer :
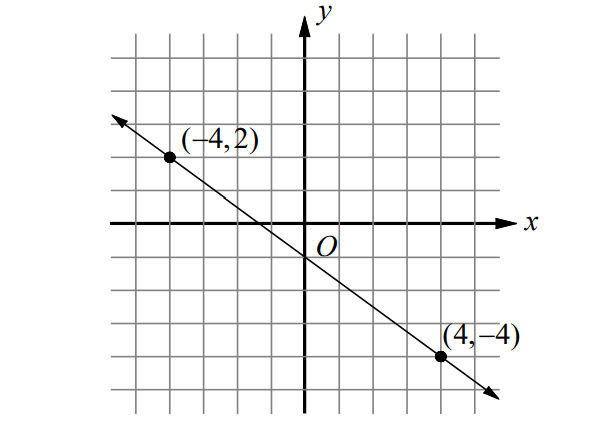
Formula to find the slope of a line when two points are given :
Substitute (x1, y1) = (-4, 2) and (x2, y2) = (4, -4).
Equation of the line in slope-intercept form :
y = mx + b
Substitute m = -3/4.
y = -3x/4 + b ----(1)
Substitute one of the two points on the line into the above equation to solve for b.
Substitute (-4, 2) into the above equation.
2 = -3(-4)/4 + b
2 = -3(-1) + b
2 = 3 + b
Subtract 3 from both sides.
-1 = b
Substitute b = -1 in (1).
y = -3x/4 - 1
Multiply both sides by 4.
y = -3x/4 - 1
4(y) = 4(-3x/4 - 1)
4(y) = 4(-3x/4) + 4(-1)
4y = -3x - 4
Add 3x to both sides.
3x + 4y = -4
7. Answer :
Equation of the line in slope-intercept form :
y = mx + b
Given : Slope is -3. So, substitute m = -3.
y = -3x + b ----(1)
Since the line passes through the point (0, -1) substitute the point (0, -1) into the above equation.
-1 = -3(0) + b
-1 = 0 + b
-1 = b
Substitute b = -1 in (1).
y = -3x + b
y = -3x - 1
Add 3x both sides.
3x + y = -1
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 04, 25 10:29 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 96)
Jan 04, 25 10:26 AM
Digital SAT Math Problems and Solutions (Part - 96) -
Simplifying Complex Fractions Problems and Solutions
Jan 04, 25 12:31 AM
Simplifying Complex Fractions Problems and Solutions