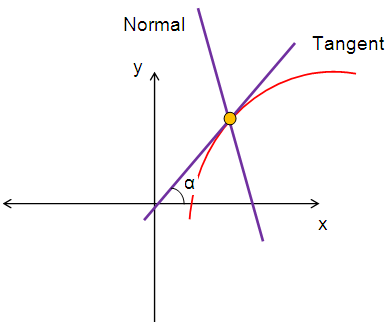
EQUATION OF NORMAL TO THE CURVE WITH DERIVATIVE

Step 1 :

By finding the first derivative, we get slope of the tangent line drawn to the curve.

Step 2 :

By applying the specific point in the general slope, we can find slope of the tangent line drawn at the specific point.

Step 3 :

From slope of tangent we have to find the slope of normal (-1/m).

Step 4 :

Now we have to apply the point and the slope in the formula

(y - y₁)  =  (-1/m) (x - x₁)

Example 1 :

Find the equation of the tangent to the curve

y  =  x³

at the point (1, 1)

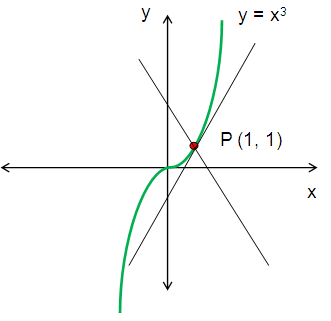
Solution :

y  =  x³

Step 1 :

dy/dx  =  3x²

slope of the curve at the point (1, 1)

dy/dx  =  3(1)²

Slope at (1, 1) :

dy/dx  =  3

Slope of normal  =  -1/3

Equation of the normal :

(y - y₁)  =  (-1/m) (x - x₁)

(y-1)  =  (-1/3) (x - 1)

3(y - 1) = -1(x - 1)

3y-3 = -x + 1

x + 3y - 3 - 1 = 0

x + 3y - 4 = 0

The required equation of normal is x+3y-4  =  0.

Example 2 :

Find the equation of normal to the curve

y  =  x²-x-2

at the point (1, -2)

Solution :

y  =  x²-x-2

dy/dx  =  2x-1

Slope at the point (1, -2) :

dy/dx  =  2(1) - 1

= 2-1

dy/dx  =  1

slope of the tangent (dy/dx) = 1

Slope of normal  =  -1/1

=  -1

Equation of the normal :

(y - y₁)  =  (-1/m) (x - x₁)

(y-(-2))  =  -1 (x-1)

y+2  =  -x+1

x+y+2-1  =  0

x+y+1  =  0

Equation of normal is x+y+1  =  0.

Example 3 :

Find a point on the curve y = √x, where the tangent makes an angle of 45 degrees with the positive x-axis.

Solution :

y  =  √x

m  =  tan θ

m  =  tan 45

m  =  1 ---(1)

dy/dx  =  1/2√x  ---(2)

(1)  =  (2)

1  =  1/2√x

2√x  =  1

4x  =  1

x  =  1/4

By applying the value of x in y  =  √x, we get

y  =  √(1/4)

y   =  ± 1/2

Since the tangent drawn at the positive x-axis, we find equation of the tangent at the point (1/4, 1/2).

Equation of the tangent line :

y - y₁ = m(x - x₁)

y - (1/2) = 1(x - 1/4)

(2y - 1)/2 = 1(4x - 1)/4

4(2y - 1) = 2(4x - 1)

8y - 4 = 8x - 2

8x - 8y - 2 + 4 = 0

8x - 8y + 2 = 0

4x - 4y + 1 = 0

So, equation of tangent is 4x - 4y + 1 = 0.

Example 4 :

Find a points on the curve y = 2x³ + 3x² - 12x + 1 where the tangent is horizontal ?

Solution :

y = 2x³ + 3x² - 12x + 1

When the tangent is horizontal, it's slope = 0

dy/dx = 2(3x²) + 3(2x) - 12(1) + 0

dy/dx = 6x² + 6x - 12

dy/dx = 0

6x² + 6x - 12 = 0

Dividing by 6, we get 

x² + x - 2 = 0

(x + 2) (x - 1) = 0

Equating each factor to 0, we get

x = -2 and x = 1

At x = -2 and x = 1, the tangent will be horizontal.

Example 5 :

If f(2) = 3 and f'(2) = 5, find the equation of the tangent line to f(x) at x = 2.

Solution :

f(2) = 3 and f'(2) = 5

The curve is passing through the point (2, 3). Slope at x = 2 is 5.

Equation of tangent :

y - y₁ = m(x - x₁)

y - 3 = 5(x - 2)

y = 5x - 10 + 3

y = 5x - 7

Example 6 :

Use the figure to the below to answer the following questions:

a) What is f (1) and f (4) ?

b) What is the geometric interpretation of

[f(4) - f(1)]/(4 - 1) ?

c)  Using the geometric interpretation of each expression, insert the proper inequality symbol (< or >)

i)  [f(4) - f(1)]/(4 - 1) ______   [f(4) - f(3)]/(4 - 3)

ii)  [f(4) - f(1)]/(4 - 1) ____ f'(1)

Solution :

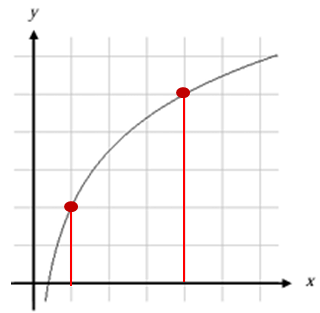
a) From the figure above

f(1) = 2 and f(4) = 5

b) [f(4) - f(1)]/(4 - 1)

Applying the values above,

= (5 - 2)/3

= 3/3

= 1

[f(4) - f(1)]/(4 - 1) = 1

c)  

i)  [f(4) - f(1)]/(4 - 1) = 1 (From above calculation)

f(3) = 4.5 (from the above figure)

[f(4) - f(3)]/(4 - 3) = (5 - 4.5)/1

= 0.5

Comparing the slopes, 1 > 0.5

ii)  [f(4) - f(1)]/(4 - 1) ____ f'(1)

 [f(4) - f(1)]/(4 - 1) = 1

[f(4) - f(1)]/(4 - 1) > f'(1)

Example 7 :

Use the graph of f (x) shown below.

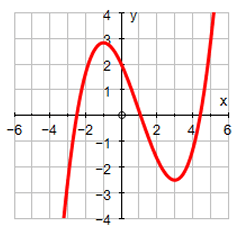
a) Where is f'(x) = 0 ?, explain.

b)  Where is f'(x) > 0 ?, explain.

c) Where is f'(x) < 0 ?, explain.

Solution :

a) From the graph above, at x = -1 and at x = 3, we draw the horizontal tangent line.  Then at x = -1 and x = 3, the slope is 0.

b) At (-∞, -1) and (3, ∞) the curve is increasing. At these intervals, the curve will have positive slope.

At (-1, 3), the curve is decreasing. So, at (-1, 3) the curve will have negative slope.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.