EQUATION OF THE LINE WHEN PARALLEL LINE AND SUM OF INTERCEPTS IS GIVEN

Question 1 :

Find the equation of a straight line parallel to 2x + 3y = 10 and which is such that the sum of its intercepts on the axes is 15

Solution :

Since the required line is parallel to the line 2x + 3y = 10 

Equation of the required line will be in the form

2x + 3y + k  =  0

Let us change the above equation to intercept form.

2x + 3y  =  -k

2x/(-k) + 3y/(-k)  =  1

x/(-k/2) + y/(-k/3)  =  1

x -intercept  =  a and y -intercept  =  b

Sum of intercepts  =  15

a + b  =  15

(-k/2) + (-k/3)  =  15

(-3k - 2k)/6  =  15

-5k/6  =  15

k  = -15(6)/5  =  -18

2x + 3y - 18  =  0

Hence the equation of the required line is 2x + 3y - 18  =  0.

Question 2 :

Find the length of the perpendicular and the co-ordinates of the foot of the perpendicular from (−10,−2) to the line x + y − 2 = 0

Solution :

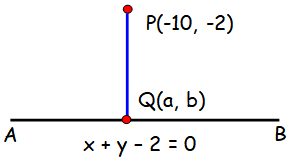
The lines PQ and AB are perpendicular to each other.

Equation of AB :

x + y - 2  =  0

Equation of PQ :

x - y + k  =  0

The point P (-10, -2) lies on the line PQ.

-10 + 2 + k  =  0

k - 8  =  0 

k  =  8

Equation of PQ is x - y + 8  = 0

By solving the equations of AB and PQ, we get the value of P.

x + y - 2  =  0  ----(1)

x - y + 8  = 0  ----(2)

(1) + (2) ==>  2x + 6  =  0  ==> x  =  -3

By applying the value of x in (1), we get the value of y.

-3 + y - 2  =  0

-5 + y  =  0

y  =  5

Hence the required point P (-3, 5)

Length of perpendicular :

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(-3+10)² + (5+2)²

  =  √7² + 7²

  =  √98  =  7√2 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.