EQUATIONS WITH THE DISTRIBUTIVE PROPERTY

In this section, we are going to see, how distributive property can be used to solve equations. 

Example  1 :

Solve for x :

4(x - 3) + 2  =  2 + x

Solution :

Step 1 : 

Use the Distributive Property.

Distribute 4 to the terms inside the parentheses.

4x - 12 + 2  =  2 + x

Simplify 

4x - 10  =  2 + x

Step 2 : 

Use inverse operations to solve the equation.

4x - 10  =  2 + x

Add 10 to each side.

4x  =  12 + x

Subtract x from each side. 

3x  =  12

Divide each side by 3.

3x / 3  =  12 / 3

x  =  4

Example 2 :

Solve for n :

0.7n + 0.33  =  0.3n + 0.5

Solution :

Step 1 :

In the second term 0.33 on the left side, we have two digits (more number of digits) after the decimal.

So, multiply both sides of the equation by 100 to get rid of the decimal point. 

100(0.7n + 0.33)  =  100(0.3n + 0.5)

Use the Distributive Property.

100(0.7n) + 100(0.33)  =  100(0.3n) + 100(0.5)

70n + 33  =  30n + 50

Step 2 :

70n + 33  =  30n + 50

Subtract 33 from each side.

70n  =  30n + 17

Subtract 30n from each side.

40n  =  17

Divide each side by 40.

n  =  17/40

n  =  0.425

Example 3 :

Solve for n : 

7n/10 + 3/2  =  3n/5 + 2

Solution :

Step 1 : 

Find the least common multiple of the denominators (10, 2 and 5).

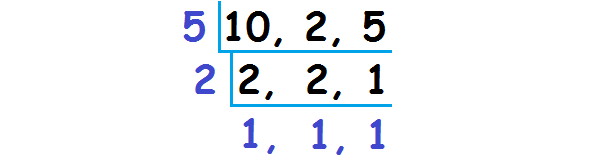
LCM  =  5 x 2 x 1 x 1 x 1

LCM  =  10

Step 2 : 

Multiply both sides of the equation by 10. 

10(7n/10 + 3/2)  =  10(3n/5 + 2)

Use distributive property.

10(7n/10) + 10(3/2)  =  10(3n/5) + 10(2)

Simplify.

7n + 5(3)  =  2(3n) + 20

7n + 15  =  6n + 20

Step 3 :

Use inverse operations to solve for 'n'.

Subtract 15 from each side. . 

7n + 15  =  6n + 20

7n  =  6n + 5

Subtract 6n from each side. 

n  =  5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.