EQUIVALENT FRACTIONS AND DECIMALS

Fractions and decimals that represent the same value are equivalent.

For example, 1//4 and 0.25 are equivalent. 

Because,

1/4  =  0.25

The number line shows some equivalent fractions and decimals from 0 to 1.

How to get decimal equivalent to a fraction ? 

To get the decimal equivalent to the fraction given, first we have to check whether the denominator of the fraction is convertible to 10 or 100 using multiplication.  

Method 1 : 

If it is convertible to 10 or 100 using multiplication, we can convert the given fraction into decimal as explained below. 

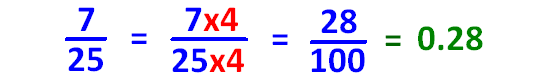
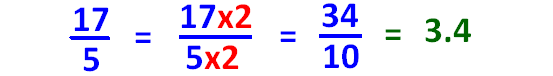
Method 2 : 

If it is not convertible to 10 or 100 using multiplication, we can get the decimal equivalent to the given fraction as explained below.  

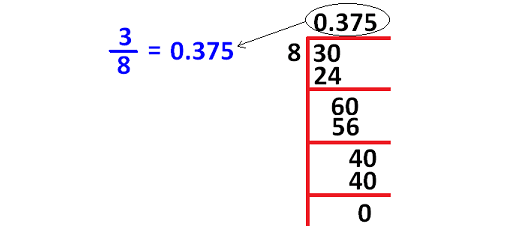
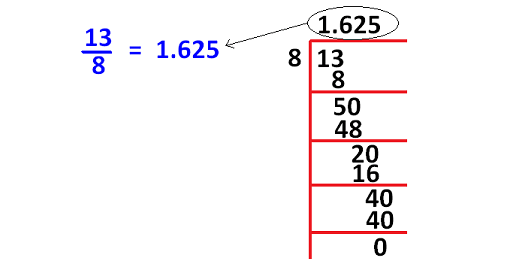
How to get fraction equivalent to a decimal ? 

To get fraction equivalent to the given decimal, first we have to count the number of digits after the decimal. 

(i) If there is only one digit after the decimal, we have to multiply and divide the decimal number by 10. 

Example :

0.2 = (0.2 ⋅ 10)/10

= 2/10

 = 1/5

(ii) If there are two digits after the decimal, we have to multiply and divide the decimal number by 100.  

Example :  

0.25 = (0.25 ⋅ 100)/100

= 25/100

 = 1/4

Note :

If there are three digits after the decimal, we have to take 1000 as denominator and so on. 

Practice Problems

Problem 1 : 

Look at the number line given below and write the missing decimals and fractions.

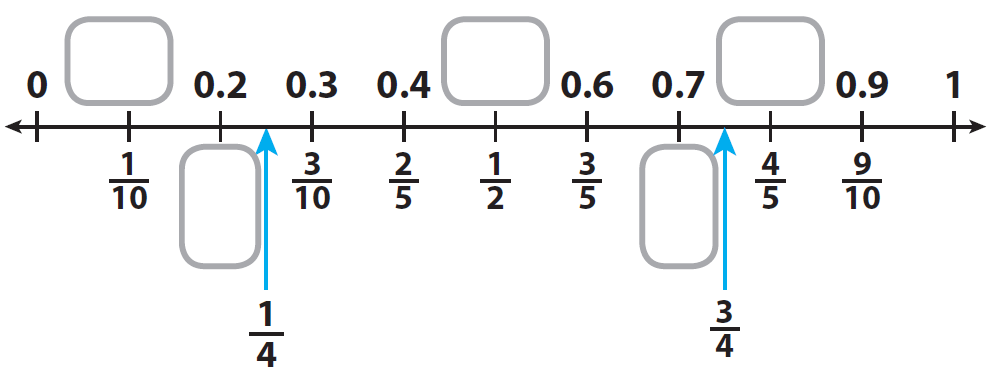
Solution :

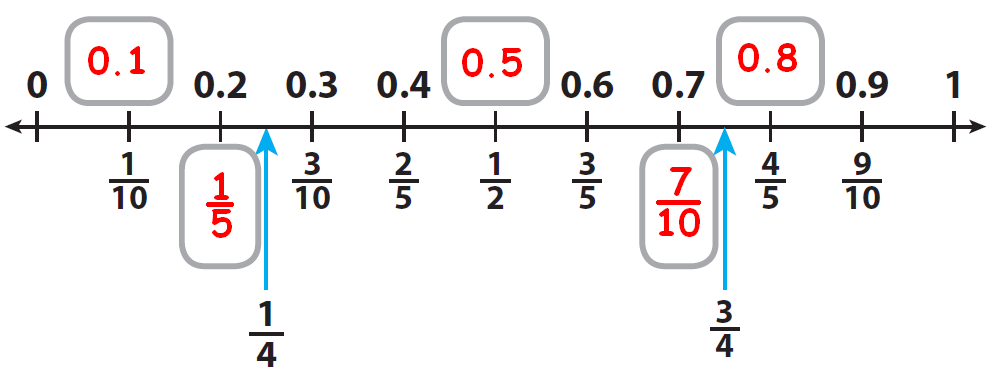
Problem 2 :

Find the decimal equivalent to the fraction given below.

3/20

Solution : 

In the given fraction, the denominator is 20 which can be converted  to 100 using multiplication by 5.

3/20 = (3 x 5)/(20 x 5)

= 15/100

= 0.15

Problem 3 :

Find the decimal equivalent to the fraction given below.

7/10

Solution : 

In the given fraction, the denominator is 10.

7/10 = 0.7 

Problem 4 :

Find the fraction equivalent to the decimal given below.

0.85

Solution : 

In the given decimal, there are two digits after the decimal.

So, we can write the given decimal as a fraction with denominator 100. 

0.85 = 85/100

= 17/20

Problem 5 :

Find the fraction equivalent to the decimal given below.

0.305

Solution : 

In the given decimal, there are three digits after the decimal.

So, we can write the given decimal as fraction with denominator 1000. 

0.305 = 305/1000

= 61/200

Problem 6 :

Fractions 15/39 and 45/117 are equivalent fractions.

Solution : 

15/39 and 45/117

To check if these two fractions are equivalent, we have to make the fractions as like fractions.

15/39 = (15/39) x (3/3)

= 45/117

So, these two fractions are like fractions.

Problem 7 :

The sum of two fractions is always a fraction.

Solution :

Yes, sum of any two fractions must be a fraction.

Problem 8 :

Write 3/4 as a fraction with the denominator of 44.

Solution : 

To make the denominator of the fraction 3/4 as 44, we have to multiply both numerator and denominator by 11.

= (3/4) x (11/11)

= 33/44

So, 3/4 = 33/44

Problem 9 :

A rectangle is divided into certain number of equal parts. If 16 of the parts so formed represent the fraction 1/4 , find the number of parts in which the rectangle has been divided.

Solution : 

Let x be the total number of parts.

So, x is being divided into 16 equal parts, then value of one part will be 1/4. 

x/16 = 1/4

To solve it, we have to do cross multiplication.

4x = 16

x = 16/4

x = 4

Problem 10 :

An MP3 player is bought for E240 and sold for E270. Find the ratio of the cost price to the selling price.

Solution : 

Problem 11 :

The maximum speeds of a boat and a car are in the ratio 2 : 7. If the maximum speed of the boat is 30 km per hour, find the maximum speed of the car.

Solution :

The maximum speed of boat = 30 km per hour

Maximum speed of boat and car is 2 : 7

Let x be the maximum speed of car.

2 : 7 = 30 : x

2/7 = 30/x

2x = 7(30)

x = 7(30)/2

x = 7(15)

= 105 km per hour.

Problem 12 :

A farmer has sheep and cattle in the ratio 8 : 3. 

a) How many sheep has the farmer if he has 180 cattle?

b) Find the ratio of the number of sheep to the total number of animals.

c) Find the ratio of the total number of animals to the number of cattle.

Solution :

Ratio between sheep and cattle = 8 : 3

Let x be the number of sheep.

180 be the number of cattle.

x : 180 = 8 : 3

x/180 = 8/3

3x = 180(8)

x = 180(8) / 3

x = 60(8)

= 480

a) Number of sheep is 480.

b)  Total number of animals = total number of sheep + total number of cattle

= 480 + 180

= 660

c)  Ratio between total number of animal to cattle.

660 : 180

= 66 : 18

= 11 : 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.