ESTIMATING IRRATIONAL NUMBERS

Irrational numbers are numbers that are not rational. In other words, they cannot be written in the form a/b, where a and b are integers and b is not 0. 

Square roots of perfect squares are rational numbers. Square roots of numbers that are not perfect squares are irrational.

The number √3 is irrational because 3 is not a perfect square of any rational number.

Estimate the Value of √2 

A. Since 2 is not a perfect square, √2 is irrational.

B. To estimate √2 , first find two consecutive perfect squares that 2 is between. We can do this by writing the following inequality. 

1 < 2 < 4

C. Now take the square root of each number.

D. Simplify the square roots of perfect squares.

√2 is between 1 and 2

E. Estimate that √2 ≈ 1.5.

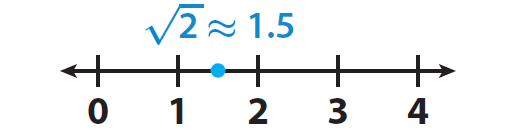
F. To find a better estimate, first choose some numbers between 1 and 2 and square them.

For example, choose 1.3, 1.4, and 1.5.

1.3² = 1.69,  1.4² = 1.96,  1.5² = 2.25

Is √2 between 1.3 and 1.4 ? How do we know ?

No ; √2 is not between 1.69 and 1.96.

Is √2 between 1.4 and 1.5 ? How do we know ?

Yes ; √2 is between 1.96 and 2.25.

Since √2 is between 1.4 and 1.5, we have √2 ≈ 1.45.

G.  Locate and label this value on the number line.

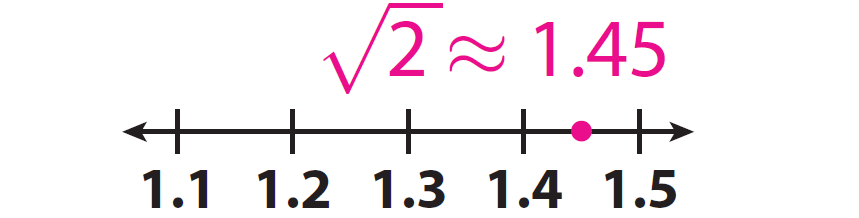
Reflect

Question 1 :

How could you find an even better estimate of √2 ?

Answer :

Test the squares of numbers between 1.4 and 1.5.

Question 2 :

Find a better estimate of √2 . Draw a number line and locate and label your estimate.

Answer :

√2 is between 1.41 and 1.42. So, √2 ≈  1.415.

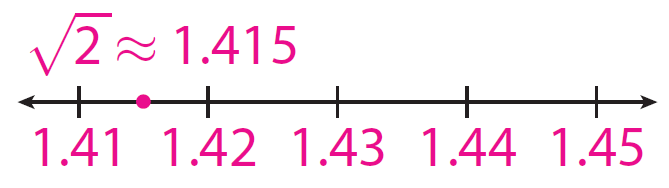
Question 3 :

Find a better estimate of √7 . Draw a number line and locate and label your estimate.

Answer :

√7 is between 2.6 and 2.7. So, √7 ≈  2.65.

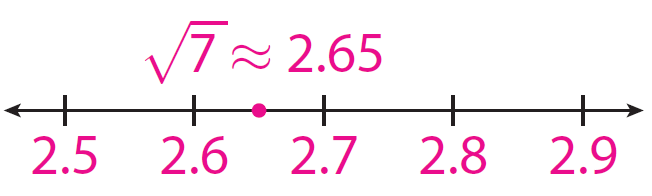
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.