EULERS TEOREM ON HOMOGENOUS FUNCTION PRACTICE PROBLEMS

In each of the following cases, determine whether the following function is homogeneous or not. If it is so, find the degree.

Problem 1 :

(i) f (x, y) = x² y + 6x³+7                 Solution

(ii)

Solution

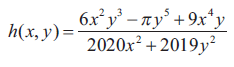
(iii) 

Solution

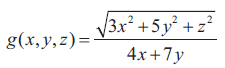
(iv)

Solution

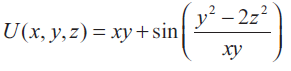
Problem 2 :

Prove that

f (x, y) = x³ − 2x²y +3xy² + y³

is homogeneous; what is the degree? Verify Euler’s Theorem for f.                Solution

Problem 3 :

Prove that

g(x, y) = x log (y/x)

is homogenous, what is the degree ? Verify Euler's  theorem for g.

Solution

Problem 4 :

Prove that

g(x, y) = x log (y/x)

is homogenous, what is the degree ? Verify Euler's  theorem for g.

Solution

Problem 5 :

If

v(x, y) = log [(x²+y²)/(x+y)]

prove that x(∂v/∂x) + y(∂v/∂y) =  1

Solution

Problem 6 :

If

w(x, y, z) = log[(5x³y⁴+7y²xz⁴-75y³z⁴)/(x²+y²)]

find x(∂w/∂x) + y(∂w/∂y) + z(∂w/∂z).

Solution

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.