EVALUATE PIECEWISE FUNCTION QUESTIONS AND ANSWERS

To evaluate the given piecewise function, we need to follow the steps given below. 

(i)  Draw number line and write the values of x, according to the given interval. 

(ii) Write the appropriate function below the corresponding interval.

(iii)  Now we have to choose the function based on the value of x we find in f(x) and evaluate.

Question 1 :

If the function f is defined by

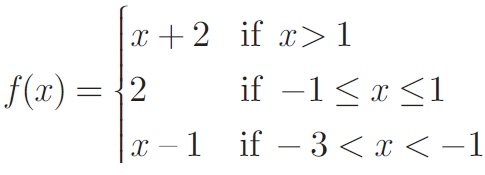
find the values of

(i) f (3) (ii) f (0) (iii) f (−1.5) (iv) f (2)+ f (−2)

Solution :

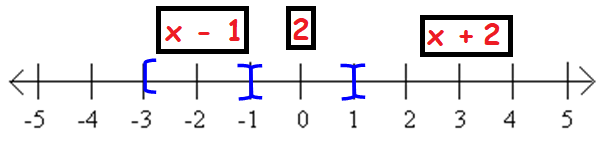
(i)  f(3)

Instead of x, we have 3. So we have to choose the function f(x)  =  x + 2

f(3)  =  3 + 2

f(3)  =  5

(ii)  f(0)

0 lies between -1 and 1. So, the answer is 2.

(iii) f (−1.5)

f(x)  =  x - 1

f(-1.5)  =  -1.5 - 1

f(-1.5)  =  -2.5

 (iv) f (2)+ f (−2)

f (2) + f (−2)  =  4 + (-3)  =  1

Question 2 :

A function f : [−5,9] -> R is defined as follows:

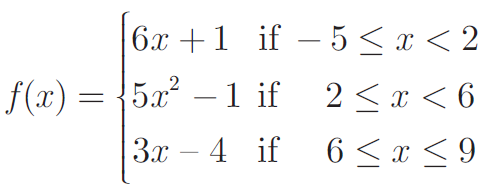
Find (i) f (−3) + f (2) (ii) f (7) - f (1) (iii) 2f (4) + f (8)

(iv)  [2f(-2) - f(6)] / [f(4) + f(-2)]

Solution :

(i) f (−3) + f(2)

f(x)  =  6x + 1 for f(-3) and f(x)  =  5x² - 1 for f(2)

f (−3) + f(2)  =  -17 + 19

f (−3) + f(2)  =  2

(ii) f (7) - f (1)

f(x)  =  3x - 4 for f(7) and f(x)  =  6x + 1  for f(1)

f (7) - f (1)  =  17 - 7  =  10

(iii) 2f (4) + f (8)

f(x)  =  5x² - 1 for f(4)  and f(x)  =  3x - 4 for f(8)

 2f (4) + f (8)  =  2(79) + 20 

  =  158 + 20

  2f (4) + f (8)  =  178

(iv)  [2f(-2) - f(6)] / [f(4) + f(-2)]

f(x)  =  6x + 1 for f(-2) and f(x) = 3x - 4 for f(6)

 [2f(-2) - f(6)] / [f(4) + f(-2)]  =  [2(-11) - 14] / [79 + (-11)]

  =  (-22 - 14) / (79 - 11)

  =  -36/68

  =  -9/17

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.