EVALUATE POLYNOMIALS USING SYNTHETIC DIVISION
An elegant way of dividing a polynomial by a linear polynomial was introduced by Paolo Ruffin in 1809. His method is known as synthetic division. It facilitates the division of a polynomial by a linear polynomial with the help of the coefficients involved.
Let us see how synthetic division can be used to explain the method of synthetic division with an example.
Let p(x) = x3 + 2x2 - x - 4 be the dividend and q(x) = x + 2 be the divisor. We shall find the quotient s(x) and the remainder r, by proceeding as follows.
Step 1 :
Arrange the dividend and the divisor according to the descending powers of x and then write the coefficients of dividend in the first row (see figure). Insert 0 for missing terms.
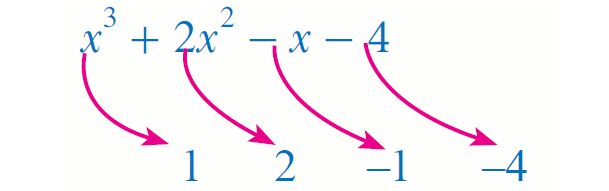
Step 2 :
Find out the zero of the divisor.
x + 2 = 0
x = -2
Step 2 :
Put 0 for the first entry in the 2nd row.
Complete the entries of the 2nd row and 3rd row as shown below.
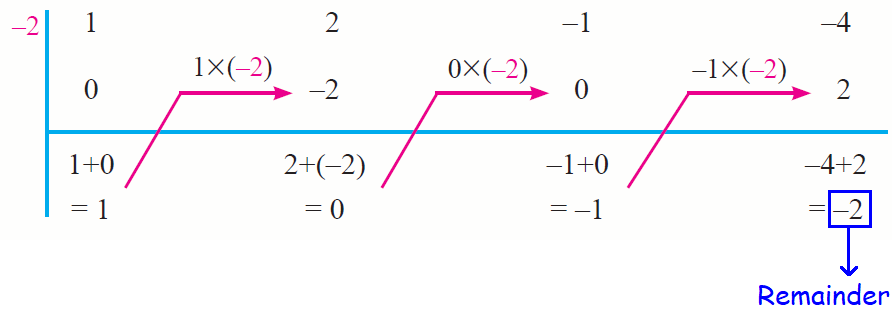
Step 4 :
Write down the quotient and the remainder accordingly. All the entries except the last one in the third row constitute the coefficients of the quotient.
Thus, the quotient is x2 - 1 and the remainder is –2.
In the above synthetic division. zero of the divisor is -2 and the remainder is -2.
This can be written as
p(-2) = -2
When we substitute the zero of the divisor -2 for x into p(x), the result is the remainder -2.
That is, evaluation of the polynomial p(x) for x = -2 is -2.
Example 1 :
If f(x) = x3 + x2 - 7x - 3, then evaluate f(3).
Solution :
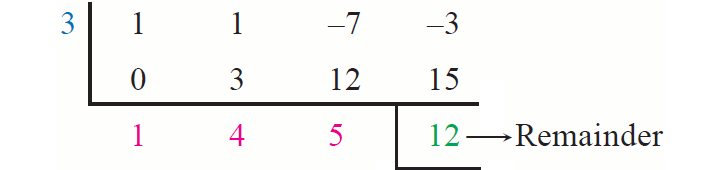
From the synthetic division above, we have
f(3) = 12
Example 2 :
If g(x) = 2x3 - 3x2 - 3x + 2, then evaluate g(-1).
Solution :
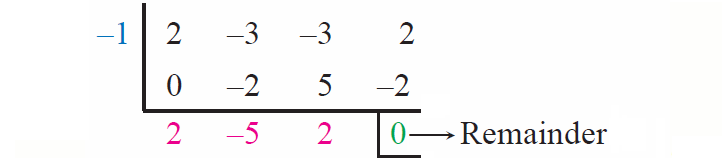
From the synthetic division above, we have
g(-1) = 0
Example 3 :
If p(x) = x3 - 3x2 - 10x + 24, then evaluate p(2).
Solution :
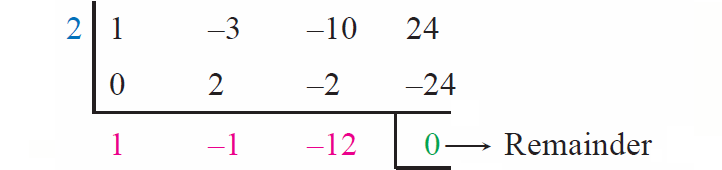
From the synthetic division above, we have
p(2) = 0
Example 4 :
If q(x) = 2x4 + x3 - 14x2 - 19x + 6, then evaluate q(-1/2).
Solution :
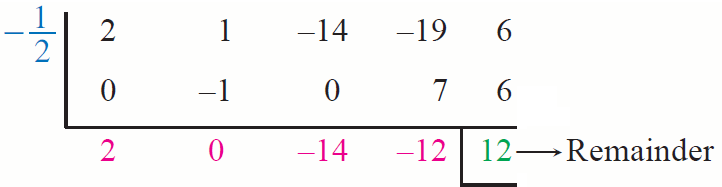
From the synthetic division above, we have
q(-1/2) = 12
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 134)
Apr 02, 25 12:40 AM
Digital SAT Math Problems and Solutions (Part - 134) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Apr 02, 25 12:35 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part 135)
Apr 02, 25 12:32 AM
Digital SAT Math Problems and Solutions (Part 135)

