Evaluate the Following Limit Using l-Hopital-s Rule

Evaluate the following limits, if necessary use l'hopital rule :

Problem 1 :

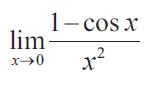
Solution :

= lim x-->0 (1 - cos x)/x²

By applying the given function, 

= (1 - cos 0)/0²

= (1 - 1)/0

= 0/0

Indeterminant form.

Differentiate the numerator and denominator, we get

= lim x-->0 [0 -(-sin x) / 2x]

= lim x-->0 (sin x / 2x)

Applying the limit, we get 0/0.

= lim x-->0 (cos x / 2(1))

= lim x-->0 cos x/2

Applying the limit, we get

= cos (0) /2

= 1/2

lim x-->0 (1 - cos x)/x² = 1/2

Problem 2 :

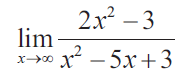
Solution :

Factoring x², we get

=  lim x-> ∞ x²(2 - 3/x²) / x²(1 - 5/x + 3/x²)

=  lim x-> ∞ (2 - 3/x²) / (1 - 5/x + 3/x²)

By applying the limit, we get

=  2/1

=  2

So, the answer is 2.

Problem 3 :

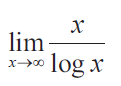
Solution :

By applying the limit, we get

=  ∞/log ∞

=  ∞/0

=  ∞

So, the answer is ∞.

Problem 4 :

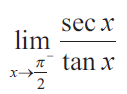
Solution :

= lim x--> π/2^- sec x / tan x

Applying the limit, we get

= sec (π/2) / tan (π/2)

= ∞/∞

Indeterminant form.

Using L'Hopital's rule, differentiate the numerator and denominator. we get 

= lim x--> π/2^- sec x tan x / sec² x

= lim x--> π/2^- tan x / sec x

= lim x--> π/2^- (sin x / cos x) / (1/cos x)

= lim x--> π/2^- (sin x / cos x) x (cos x / 1)

= lim x--> π/2^- sin x

Applying the limit, we get

= sin (π/2)

= 1

So, the value of lim x--> π/2^- sec x / tan x is 1.

Problem 5 :

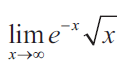
Solution :

= lim x--> ∞ e^-x √x

The given function is not in the form of f(x) / g(x)

= lim x--> ∞ (√x / e^x)

Applying the limit, we get

= (√∞ / e^∞)

= ∞/∞

Indeterminant form.

Differentiate the numerator and denominator separately, we get

=  lim x--> ∞ (1/2√x / e^x)

=  lim x--> ∞ (1/2√∞ / e^∞)

= 1/2(∞) / ∞

= 0/∞

= 0

So, the answer is 0.

Problem 6 :

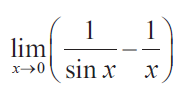
Solution :

= lim x--> 0 (1/sin x - 1/x)

The given function is not in the form of f(x)/g(x).

= lim x--> 0 (x - sin x)/x sin x

Applying the limit, we get

= (0 - sin 0)/0 sin 0

= 0/0

Indeterminant form. 

Differentiate the numerator and denominator, we get

= lim x--> 0 [(1 - cos x)] / [x cos x + sin x(1)]

= lim x--> 0 [(1 - cos x)] / [x cos x + sin x]

Applying the limit, we get

= 0/0

Differentiating the numerator :

= (0 - (-sin x))]

= sin x

Differentiating the denominator :

= x (-sin x) + cos x (1) + cos x

= -x sin x + cos x + cos x

= -x sin x + 2 cos x

= lim x--> 0 sin x/ (-x sin x + 2 cos x)

Applying the limit, we get

= sin 0/2 cos 0

= 0/2(1)

= 0

So, the value of lim x--> 0 (1/sin x - 1/x) is 0.

Problem 7 :

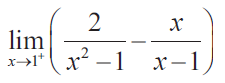
Solution :

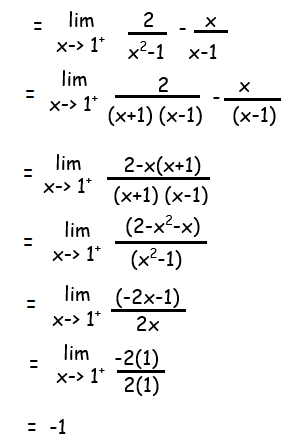
So, the answer is -1.

Problem 8 :

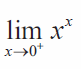
Solution :

Let f(x)  =  x^x

y  =  x^x

log y  =  log x^x

log y  =  x log x

log y  =  log x / (1/x)

lim _x->0+ log y  =  lim _x->0+ log x / (1/x)

lim _x->0+ log y  =   ∞/∞ (Indeterminant form)

Using L'Hopital's rule :

lim _x->0+ log y  =  lim _x->0+ (1/x) / (-1/x²)

lim _x->0+ log y  =  lim _x->0+ -x

By applying limit, we get

lim _x->0+ log y  =  0

log (lim _x->0+y)  =  0

(lim _x->0+y)  =  e⁰

lim _x->0+ y  =  1

So, the answer is 1.

Problem 9 :

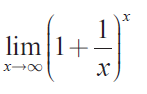
Solution :

Let f(x)  =  (1 + (1/x))^x

y  =  (1 + (1/x))^x

log y  =  log (1 + (1/x))^x

log y  =  x log (1 + (1/x))

log y  =  log (1 + (1/x)) / (1/x)

lim _{x ->∞} log y  =  lim _{x ->∞} log (1 + (1/x)) / (1/x) 

By applying the limit, we get

lim _{x ->∞} log y  =  lim _{x ->∞} log (1 + (1/∞)) / (1/∞)

lim _{x ->∞} log y  =  lim _{x ->∞} log (1)/0

lim _{x ->∞} log y  =  0/0 (Indeterminant form) 

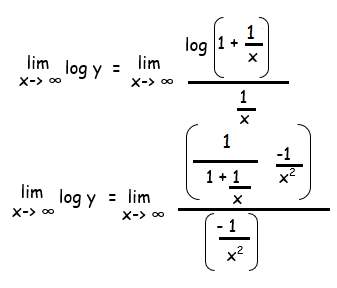
By applying the limit, we get

lim _{x ->∞} log y  =  1

log (lim _{x ->∞} y)  =  1

lim _{x ->∞} y  =  e

Problem 10 :

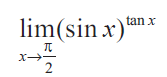
Solution :

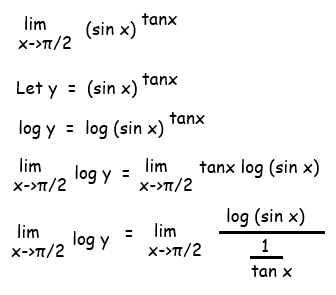
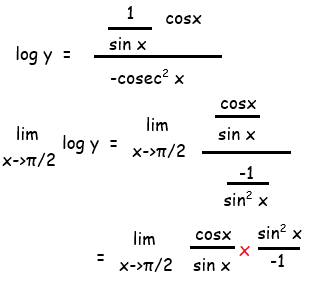
lim x->π/2  log y  =  lim x->π/2 (- sinx cosx)

By applying the limit, we get

lim x->π/2  log y  =  -sin(π/2) cos(π/2)

lim x->π/2  log y  =  1(0)

lim x->π/2  log y  =  0

log y (lim x->π/2  y)  =  0

(lim x->π/2  y)  =  1

So, the answer is 1.

Problem 11 :

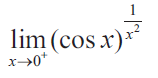
Solution :

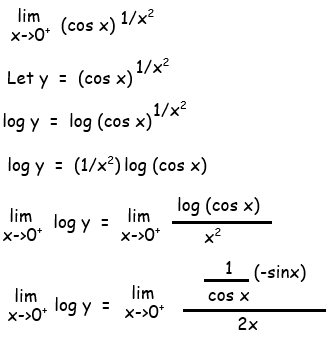
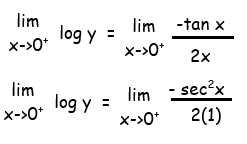
By applying the limit, we get

lim x->0⁺ log y  =  -1/2

log(lim x->0⁺ y)  =  -1/2

lim x->0⁺ y  =  e^-1/2

lim x->0⁺ y  =  1/√e

So, the answer is 1/√e.

Problem 12 :

If an initial amount A₀ of money is invested at an interest rate r compounded n times a year, the value of the investment after t years is

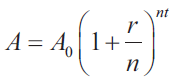
If the interest is compounded continuously, (that is as n->∞), show that the amount after t years is A = A₀ e^rt

Solution :

A  =  A₀ (1+ r/n)^nt

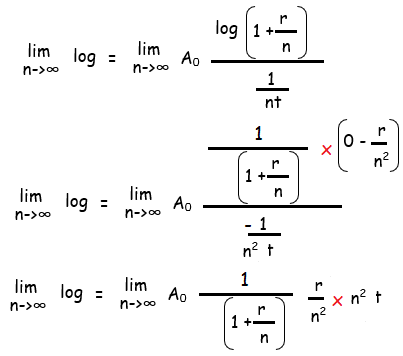
By applying the limit, we get

log (lim n->∞ y)  =  rt

lim n->∞ y  =  e^rt

A = A₀ e^rt

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.