EVALUATE THE FUNCTION FOR THE GIVEN VALUES OF X

Question 1 :

Given the function f : x -> x² −5x + 6 , evaluate

(i) f (-1)

(ii) f (2a)

(iii) f (2)

(iv) f (x −1)

Solution :

Given that :

f(x)  =  x² −5x + 6

(i) f (-1)

here we have -1 instead of x.

f(-1)  =  (-1)² −5(-1) + 6

  =  1 + 5 + 6

f(-1)  =  12

(ii) f (2a)

here we have 2a instead of x.

f(2a)  =  (2a)² −5(2a) + 6

  =  4a² - 10a + 6

(iii) f (2)

here we have 2 instead of x.

f(2)  =  (2)² −5(2) + 6

  =  4 - 10 + 6

=  0

(iv) f (x −1)

here we have x - 1 instead of x.

f(x-1)  =  (x-1)² −5(x-1) + 6

  =  x² - 2x + 1 - 5x + 5 + 6

=  x² - 7x + 12

Question 2 :

A graph representing the function f (x) is given figure

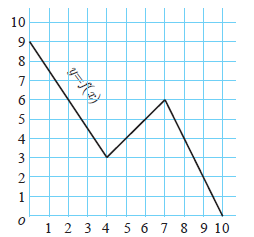
it is clear that f (9) = 2.

(i) Find the following values of the function

(a) f (0) (b) f (7) (c) f (2) (d) f (10)

(ii) For what value of x is f (x) = 1?

(iii) Describe the following (i) Domain (ii) Range.

(iv) What is the image of 6 under f ?

Solution :

(i)  

(a)  f(0)  =  9,  (b)  f(7)  =  6,  (c) f (2)  =  6,  (d) f (10)  =  0

(ii) For what value of x is f (x) = 1 ?

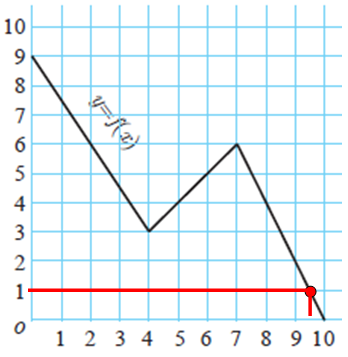
For x = 9.5, we get 1.

(iii) Describe the following (i) Domain (ii) Range.

Domain  =  { 0 ≤ x  ≤ 10 }

Range  =  { 0 ≤ x  ≤ 9 }

(iv) What is the image of 6 under f ?

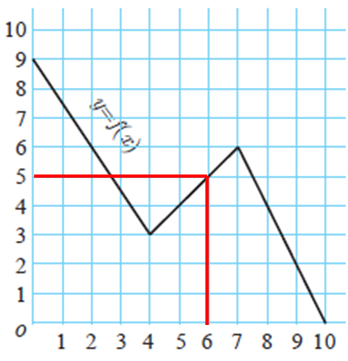
Question 3 :

Let f (x) = 2x + 5. If x ≠ 0 then find [f(x + 2) - f(2)] / x

Solution :

f (x) = 2x + 5

f(x + 2)  =  2(x + 2) + 5

f(x + 2)  =  2x + 4 + 5   -------(1)

f(x + 2)  =  2x + 9

f(2)  =  2(2) + 5 

  =  4 + 5

f(2)  =  9  -------(2)

(1) - (2)   =  2x + 9 - 9

  =  2x

[f(x + 2)  - f(2) ]/x  =  2x / x  =  2

Question 4 :

A function f is defined by f (x) = 2x – 3

(i) find [f(0) +  f(1)]/2

(ii) find x such that f (x) = 0.

(iii) find x such that f (x) = x .

(iv) find x such that f (x) = f (1−x) .

Solution :

f(x) = 2x – 3

(i)  [f(0) +  f(1)]/2

f(0)  =  2(0) - 3  =  -3

f(1)  =  2(1) - 3  =  -1

[f(0) +  f(1)]/2  =  [-3 + (-1)] / 2

  =  -4/2

  =  -2

Hence the answer is -2.

(ii) find x such that f (x) = 0.

f(x) = 2x – 3

2x - 3  =  0

2x  =  3

x  =  3/2 

Hence the answer is 3/2.

(iii) find x such that f (x) = x .

f(x) = 2x – 3

2x - 3  =  x

2x - x  =  3

x  =  3

Hence the answer is 3

(iv) find x such that f (x) = f (1−x) .

f(1 - x)  =  2(1- x) - 3

  =  2 - 2x - 3

  =  -2x - 1

2x - 3  =  -2x - 1

2x + 2x  =  - 1 + 3

4x  =  2

x  =  2/4  =  1/2

Hence the answer is 1/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.