EVALUATE THE TRIG FUNCTIONS WITH TRIG RATIOS

Question 1 :

If cos θ : sin θ = 1 : 2, then find the value of (8 cos θ - 2 sin θ)/(4 cos θ + 2 sin θ)

Solution :

Given that :

cos θ : sin θ = 1 : 2

cos θ/sin θ = 1/2

cot θ  =  1/2  =  Adjacent side / Opposite side

(Hypotenuse side)²  =  (Opposite side)² + (Adjacent side)²

  =  1² + 2²

(Hypotenuse side)²  =  5

Hypotenuse side  =  √5

sin θ  =  1/√5, cos θ = 2/√5

(8 cos θ - 2 sin θ)/(4 cos θ + 2 sin θ) 

=  (8/√5) - (4/√5)/(4/√5) + 2(2/√5)

=   (4/√5)/(8/√5)

=  4/8

  =  1/2

Question 2 :

From the given figure, prove that θ + Φ = 90°.Also prove that there are two other right angled triangles. Find sin a, cos β and tan Φ.

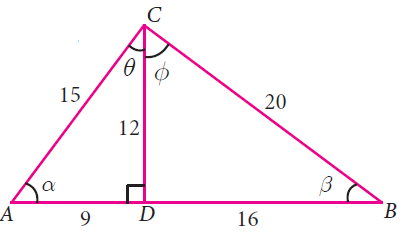
Solution :

In triangle ACD,

sin a  =  Opposite side / Hypotenuse side

sin a  =  DC/AC

sin a  =  12/15  =  4/5

In triangle BDC,

cos β  =  Adjacent side / Hypotenuse side

   =  DB/BC

cos β  =  16/20  =  4/5

tan Φ  =  Opposite side /  Adjacent side

tan Φ  =  DB/DC  =  16/12

  =  4/3

Question 3 :

A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)

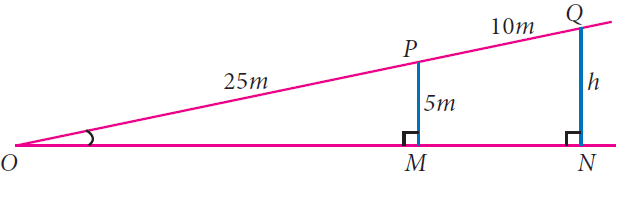
Solution :

In triangle OPM,

tan θ  =  PM/OP

=  5/25  ---(1)

tan θ  =  ON / (OP + PQ)

=  h/(25 + 10)

=  h/35  ---(2)

(1)  =  (2)

5/25  =  h/35

(1/5)(35)  =  h

h  =  7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.