EVALUATING FUNCTIONS FOR THE GIVEN VALUE OF X

About "Evaluating Functions for the Given Value x"

Evaluating Functions for the Given Value x :

Here we are going to see, how to evaluate the function for the given values of x.

Evaluate the Function at Each Specified Value - Examples

Question 1 :

If f(x)  =  (x + 2)/(x² + 1) For every real number x. Evaluate the following expression.

(i)  f(2a)    (ii)  f(2a - 1)    (iii)  f(x² + 1)    (iv)  f(2x² + 3)

Solution :

(i)  f(2a)

f(x)  =  (x + 2)/(x² + 1)

x  =  2a

f(2a)  =  (2a + 2)/((2a)² + 1)

  =  (2a + 2)/(4a² + 1)

  =  2(a + 1)/(4a² + 1)

(ii)  f(2a - 1) 

f(x)  =  (x + 2)/(x² + 1)

x  =  2a - 1

f(2a - 1)  =  (2a - 1 + 2)/((2a - 1)² + 1)

  =  (2a + 1)/(4a² + 1 + 4a + 1)

  =  (2a + 1)/(4a² + 4a + 2)

(iii)  f(x² + 1)   

f(x)  =  (x + 2)/(x² + 1)

x  =  x² + 1

f(x² + 1)  =  (x² + 1 + 2)/((x² + 1)² + 1)

=  (x² + 3)/(x⁴ + 2x² + 1 + 1)

=  (x² + 3)/(x⁴ + 2x² + 2)

(iv)  f(2x² + 3)

f(x)  =  (x + 2)/(x² + 1)

x  =  2x² + 3

f(2x² + 3)  =  (2x² + 3 + 2)/((2x² + 3)² + 1)

=  (2x² + 5)/(4x⁴ + 12x² + 9 + 1)

=  (2x² + 5)/(4x⁴ + 12x² + 10)

Question 2 :

If g(x)  =  (x - 1)/(x + 2) For every real number x. Evaluate the following expression.

(i)  Find a number "b" such that g(b) = 4.

(ii)  Find a number b such that g(b) = 3

(iii) Evaluate and simplify the expression [g(x)−g(3)]/(x−3)

Solution :

(i)  Find a number "b" such that g(b) = 4.

 g(x)  =  (x - 1)/(x + 2)

 g(b)  =  (b - 1)/(b + 2)

 4  =  (b - 1)/(b + 2)

4(b + 2)  =  b - 1

4b + 8  =  b - 1

4b - b  =  -1 - 8

3b  =  -9

b  =  -3

(ii)  Find a number b such that g(b) = 3

 g(x)  =  (x - 1)/(x + 2)

 g(b)  =  (b - 1)/(b + 2)

3  =  (b - 1)/(b + 2)

3(b + 2)  =  b - 1

3b + 6  =  b - 1

3b - b  =  -1 - 6

2b  =  -7

b  =  -7/2

(iii) Evaluate and simplify the expression [g(x)−g(3)]/(x−3)

g(x)  =  (x - 1)/(x + 2)

 g(3)  =  (3 - 1)/(3 + 2)  =  2/5

[g(x)−g(3)]/(x−3)  =  [(x - 1)/(x + 2) - (2/5)]/(x−3) 

=  [5(x - 1) - 2(x + 2)/5(x + 2)]/(x−3) 

=  [(5x - 5 - 2x - 4)/5(x + 2)]/(x−3) 

=  [(3x - 9)/5(x + 2)]/(x−3) 

=  [3 (x - 3)/5(x + 2)]/(x−3) 

=  3/5(x + 2) 

Question 3 :

Assume that f is the function defined by

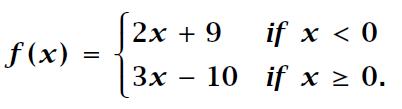
(i)  Evaluate f(2).

(ii)  Evaluate f(−3).

(iii)  Evaluate f(|x| + 1).

(iv)  Evaluate f(|x − 5| + 2).

Solution :

(i)  f(2)

Here the value of x is 2 which is greater than 0. So we have to choose the function f(x)  =  3x - 10

f(2)  =  3(2) - 10  =  6 - 10

  f(2)  =  -4

(ii)  Evaluate f(−3).

Here the value of x is 2 which is lesser than 0. So we have to choose the function f(x)  =  2x + 9

f(-3)  =  2(-3) - 9  =  - 6 - 9

  f(-3)  =  -15

(iii)  Evaluate f(|x| + 1)

f(|x| + 1)  =  3(|x|+ 1) - 10

=  3|x| + 3 - 10

f(|x| + 1)  =  3|x| - 10

(iv)  Evaluate f(|x − 5| + 2).

f(|x - 5| + 2)  =  3(|x - 5|+ 2) - 10

=  3|x - 5| + 6 - 10

f(|x - 5| + 2)  =  3|x - 5| - 4

After having gone through the stuff given above, we hope that the students would have understood "Evaluating Functions for the Given Value x". 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.