EVALUATING INVERSE TRIGONOMETRIC FUNCTIONS

If we restrict the domain of

y  =  sinx

to the interval [-π/2, π/2] as shown below

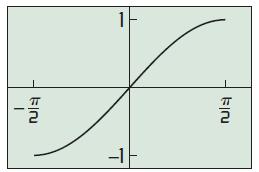
the restricted function is one to one. The inverse sine function y  =  sin^-1x is the inverse of the restricted portion of sine function.

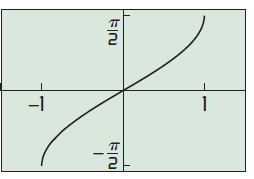
This is common for all other trigonometric ratios.

Domain and Range of Inverse sin cos tan

The following will be useful, when we find general solution or more than one solution with in the given interval.

Question 1 :

Find the exact value of sin^-1(-1/2)

Solution :

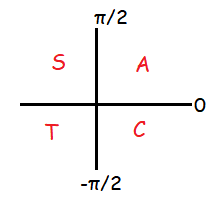
In first and fourth quadrants, we get negative values for inverse of sin function in fourth quadrant only.

If we ignore negative sign, for sin 30 degree, we get the value 1/2.

If we calculate the angle like this,

So, sin^-1(-1/2)  =   -π/6

Question 2 :

Find the exact value of cos^-1(-√2/2)

Solution :

In second quadrant, we will have negative for cosine function.

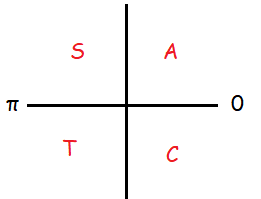
Required angle  =  π - π/4

  =  3π/4

The exact value of cos^-1(-√2/2) is 3π/4.

Question 3 :

Find the exact value of tan^-1(-1)

Solution :

In fourth quadrant, we will have negative for tangent function.

Required angle  =  -π/2 + π/4

  =  -π/2

So the exact value of tan^-1(-1) is -π/2.

Question 4 :

Find the exact value of cos^-1(-√3/2)

Solution :

In second quadrant, we will have negative for cosine function.

Required angle  =  π - π/6

  =  5π/6

So, the exact value of cos^-1(-√3/2) is 5π/6.

Question 5 :

Find the exact value of sin^-1(-1/√2)

Solution :

In first and fourth quadrants, we get negative values only in fourth quadrant.

If we ignore negative sign, for sin 45 degree, we get the value 1/√2.

Required angle  =  -π/2 + π/4

  =  -π/4

So, the exact value of sin^-1(-1/√2) is -π/4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.