EVALUATING LIMITS FOR RATIONAL FUNCTIONS

Evaluating Limits for Rational Functions at a Finite Value

When you evaluate limit for a rational function at a finite value, follow the steps given below.

Step 1 :

Factor the expressions in numerator and denominator.

Step 2 :

Cancel out the common factors.

Step 3 :

Substitute the given limit for the variable and evaluate it.

Evaluating Limits for Rational Functions at Infinity

When you evaluate limit for a rational function at infinity, follow the steps given below.

Step 1 :

Look at the highest exponent of the variable in the given rational function.

Step 2 :

Factor the variable with the highest exponent out in both numerator and denominator.

Step 3 :

Simplify and evaluate the limit.

Using the following algebraic identity, (x³ - 8) can be factored.

a³ - b³ = (a - b)(a² + ab + b²)

Since (x - 2) is the denominator of the given rational function, one of the factors of (x⁵ - 32) may be (x - 2).

We can check this by dividing (x⁵ - 32) by (x - 2) using synthetic division.

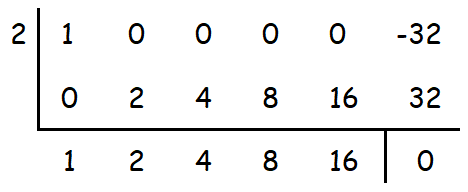
When we divide (x⁵ - 32) by (x - 2), the remainder is 0. So, (x - 2) is a factor of (x⁵ - 32).

The factored form of (x⁵ - 32) is

(x - 2)(x⁴ + 2x³ + 4x² + 8x + 16)

Since (x + 1) is the denominator of the given rational function, one of the factors of (x⁴ + 3x³ - x² + x + 4) may be (x + 1).

We can check this by dividing (x⁴ + 3x³ - x² + x + 4) by (x + 1) using synthetic division.

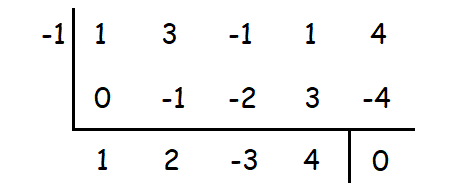
When we divide (x⁴ + 3x³ - x² + x + 4) by (x + 1), the remainder is 0.

So, (x + 1) is a factor of (x⁴ + 3x³ - x² + x + 4).

The factored form of (x⁴ + 3x³ - x² + x + 4) is

(x + 1)(x³ + 2x² - 3x + 4)

©All rights reserved. onlinemath4all.com